2022年下期 過去問 理論

このページでは、2022年下期電験三種試験の理論科目の解説を掲載しています。
問01:静電気
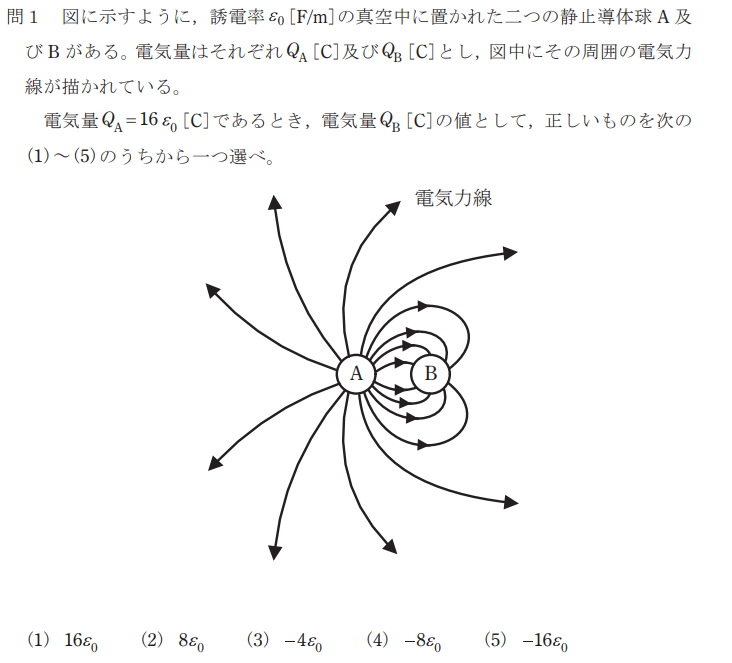
問題
解説
電気力線は正電荷から負電荷に流れることから、Bは負電荷であることが分かる。
よって、選択肢から(3)(4)(5)の何れかが正解だと判断できる。
次にAから16本の電気力線が出ており、そのうち8本がBに入っているため、Bの電気力線の本数は8本であることがわかる。
電気力線の本数は\(N=\frac{Q}{ε}\)※したがって、\(Q=Nε\)※であるため、この式に当てはめると、Bの電気量は\(-8ε_0\)となる。
したがって、答えは(4)となる。
※以下参照

問02:静電気
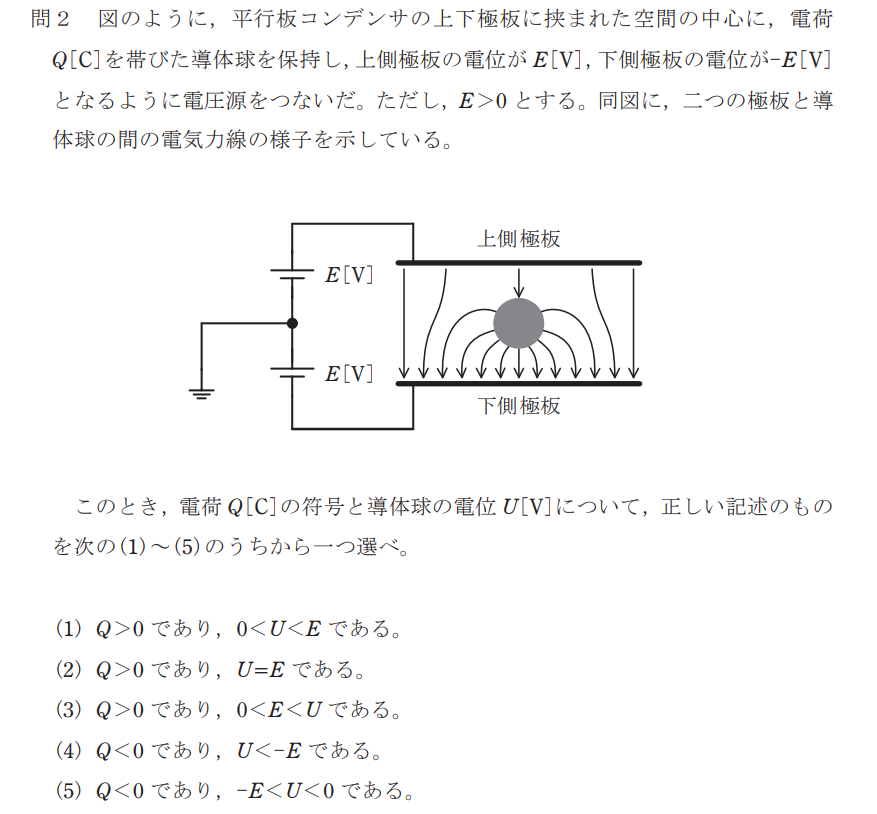
問題
解説
始めに電荷Qの符号について考える。上側極板から電荷Qに電気力線が1本入っており、電荷Qから下側極板に電気力線が複数出ていることから、電荷Qは+に帯電していることが分かる(Q>0)。
*電気力線は+から―に流れる。すなわち、電気力線を出す量の方が多い電荷Qは+であると分かる。
次に導体球の電位Uについて考える。
電気力線の方向=電界の方向である。また、電界は方向は電位の高い所から低い所となるため、電荷Qの電位は上側極板の電位より低く、下側極板の電位より高いことが分かる。
したがって、答えは(1)となる。
※以下参照

問03:電磁気
問題

解説
(ア)磁界の向きと一致するのは、N極である。
(イ)直線状導体に直流電流を流すと、導線に垂直な平面内で、導線を中心とする同心円状の磁場ができる。※
(ウ)磁力線
(エ)直線状導体の磁界の強さは\(H = \frac {I}{2πr}\)※より求められるため、距離の1乗に反比例する。
したがって、答えは(4)となる。
※以下参照

問04:電磁気
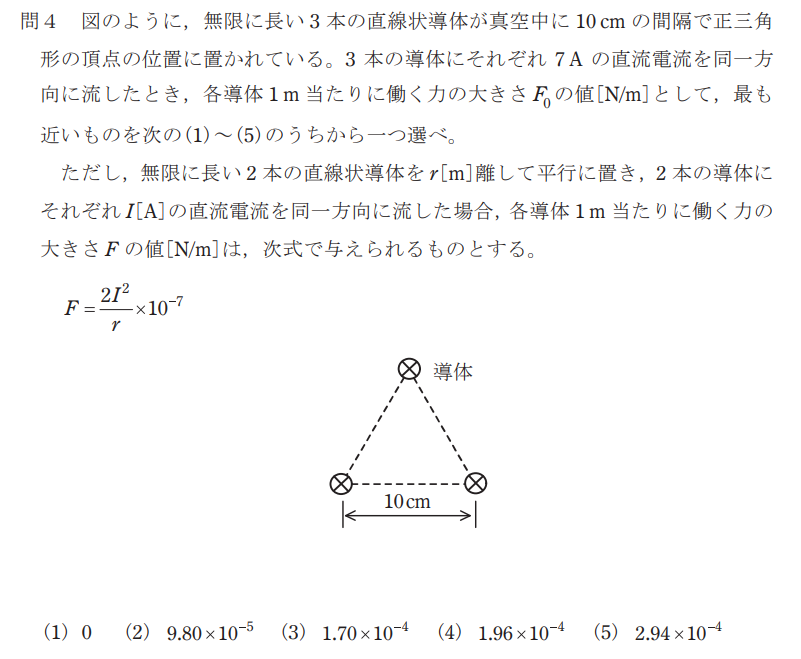
問題
解説
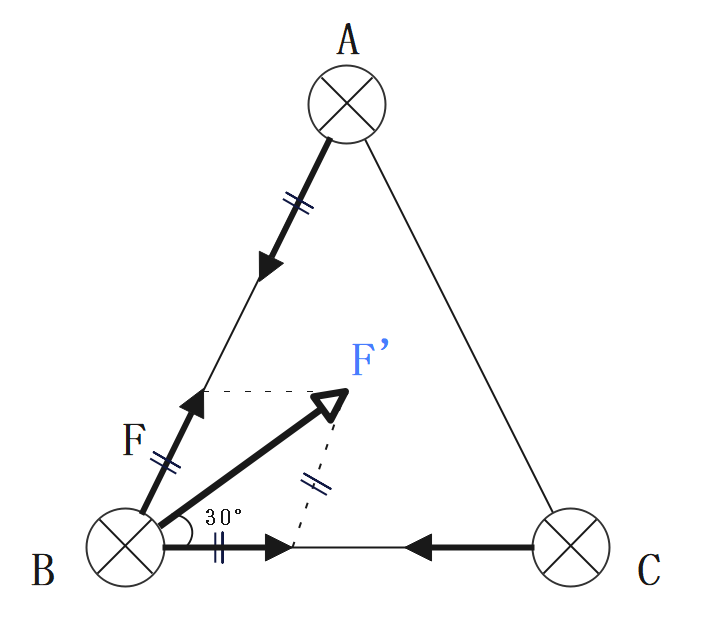
始めに各導体は同一方向に電流が流れているため、2本の導体間には吸引力F※が働く。
吸引力Fは問題文より、
$$F=\frac{2I^2}{r}×10^{-7}=\frac{2×7^2}{0.1}×10^{-7}=0.98×10^{-4}$$
次に各導体間に働く力は、それぞれの導体間に働く吸引力Fの合成力である。
よって
$$F’=F×\sqrt{3}=0.98×10^{-4}×\sqrt{3}≒1.70×10^{-4}$$
したがって、答えは(3)となる。
※以下参照

問05:直流回路
問題
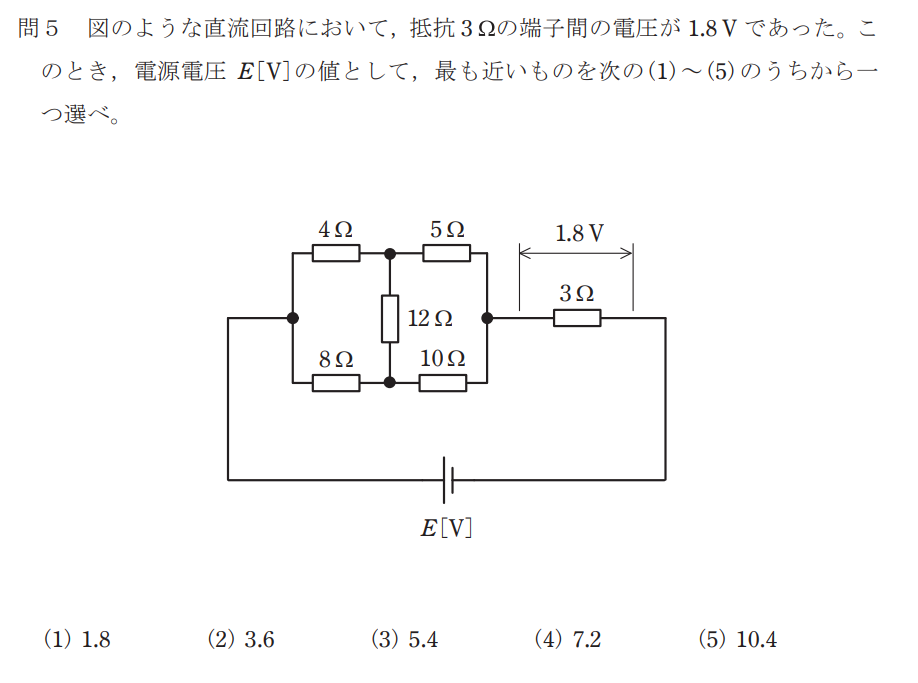
解説
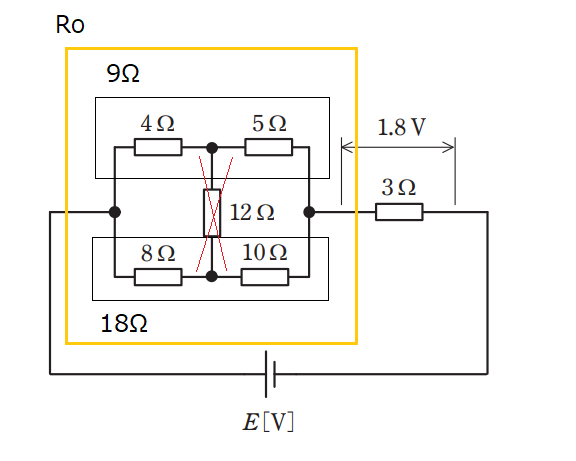
並列回路のブリッジ回路は平衡条件を満たしているため、12Ωの抵抗には電流が流れず開放できる。※
また、並列箇所の合成抵抗は、
$$R_O=\frac{9×6}{9+6}=6$$※
より、6Ωとなる。
よって、直列回路の分圧の式
$$1.8=E×\frac{3}{9+8} ⇒ E=5.4※
より、E=5.4 [V]と求められる。
したがって、答えは(3)となる。
※以下参照

問06:静電気
問題
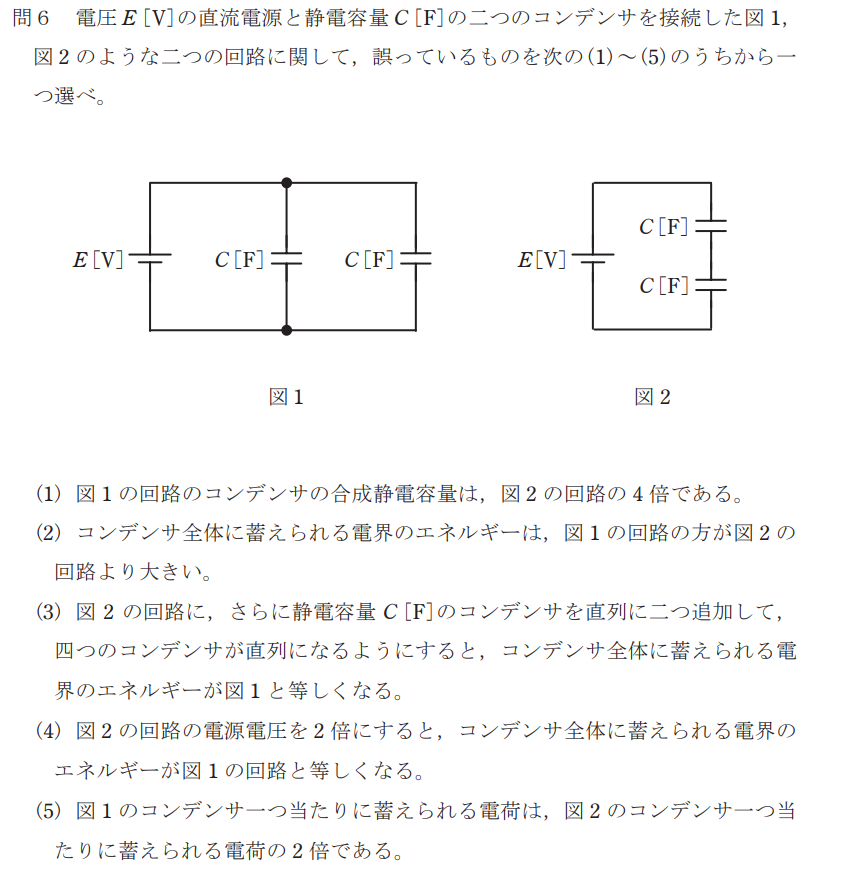
解説
(1)図1は並列回路であることから、コンデンサの合成静電容量※は、
$$C_{1}=C+C=2C$$
図2は直列回路であることから、コンデンサの合成静電容量※は、
$$C_{2}=\frac{C×C}{C+C}=\frac{1}{2}C$$
よって、(1)は正しい
(2)電界のエネルギー※は次の式で求められる。
$$W=\frac{1}{2}CV^2$$
よって、(1)で求めた合成静電容量から、図1の電界のエネルギーは、
$$W=\frac{1}{2}2CE^2=CE^2$$
また、図1の電界のエネルギーは、
$$W=\frac{1}{2}\frac{C}{2}E^2=\frac{1}{4}CE^2$$
よって、(2)は正しい
(3)静電容量Cのコンデンサを4つ直列で並べると、図2の合成静電容量は、
$$\frac{1}{\frac{1}{C}+\frac{1}{C}+\frac{1}{C}+\frac{1}{C}}=\frac{1}{4}C$$
よって、図2の電界のエネルギーは、
$$W=\frac{1}{2}\frac{1}{4}CE^2=\frac{1}{8}CE^2$$
よって、(3)は正しくない。
(4)図2の電源電圧を2倍にすると、図2の電界のエネルギーは、
$$W=\frac{1}{2}\frac{C}{2}{2E}^2=CE^2$$
よって、(4)は正しい
(5)図1は並列回路であることから、コンデンサの電荷量※は、
$$Q_1=CV=2CV$$
並列回路の各コンデンサは電荷量が等しい※ため、1つ当たりのコンデンサの電荷量は、
$$Q’_1=CV$$
図2は直列回路であることから、コンデンサの電荷量※は、
$$Q_2=\frac{1}{2}CV$$
直列回路の各コンデンサの電荷量は和である※ため、1つ当たりのコンデンサの電荷量は、
$$Q’_2=\frac{1}{2}CV$$
よって、(5)は正しい
※以下参照

問07:直流回路
問題

解説
温度変化による抵抗値の変化の式※は次の式で求められる。
$$R’=R(1+α(t_2-2_1))$$
上式を使って、21℃の時の各抵抗値を求めると、
$$R’_1=R_1(1+α_1(21-20))=R_1+α_1R_1$$
$$R’_2=R_2(1+0(21-20))=R_2$$
次に並列回路の合成抵抗の式より、各抵抗値を求めると、
$$r_{20}=\frac{R_1R_2}{R_1+R_2}$$
$$r_{21}=\frac{R’_1R’_2}{R’_1+R’_2}=\frac{(R_1+α_1R_1)R’_2}{ R_1+α_1R_1+R’_2}$$
よって、変化率は、
$$\frac{r_{21}-r_{20}}{r_{20}}=\frac{\frac{(R_1+α_1R_1)R’_2}{R_1+α_1R_1+R’_2}-\frac{R_1R_2}{R_1+R_2}}{\frac{R_1R_2}{R_1+R_2}}=\frac{α_1R_2}{R_1+R_2+α_1R_1}$$
したがって、答えは(2)となる。
※以下参照

問08:過渡現象
問題

解説
(ア)波形率は\(波形率=\frac{実効値}{平均値}\)※で、求められる。
(イ)波形が三角波のようにとがっていれば、波形率の値は大きくなる。
(ウ)波形が正弦波のように平らであれば、波形率の値は小さくなる。
(エ)波高率は\(波高率=\frac{最大値}{実効値}\)※で、求められる。
(オ)波形が三角波のようにとがっていれば、波高率の値は大きくなる。
(カ)波形が正弦波のように平らであれば、波高率の値は小さくなる。
したがって、答えは(1)となる。
※以下参照

問09:交流回路
問題
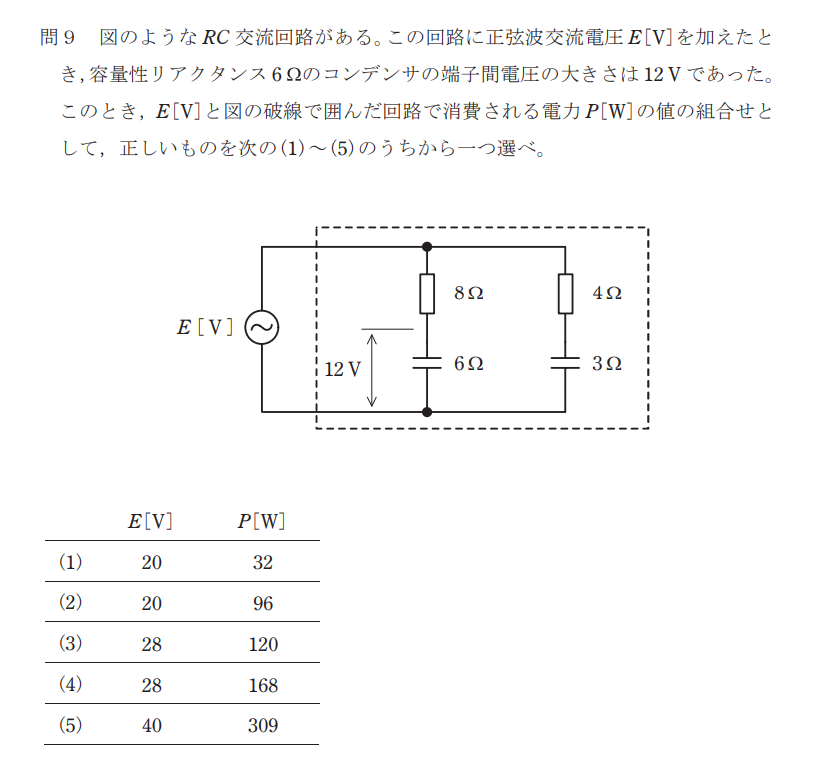
解説
8Ωと6Ωに流れる電流の大きさは等しい。よって、8Ωの電位差は
$$V_8=R_8I_1=R_8\frac{V_6}{X_{C6}}=8\frac{12}{6}=16[V]$$
また、電源電圧は抵抗、リアクタンスの両端の電位差の合成※であるため、
$$E=\sqrt{{V_8}^2+{V_{C6}}^2}=\sqrt{16^2+12^2}=20[V]$$
次に4 Ωの抵抗と3Ωのリアクタンスの大きさの比率は 4:3 であるため,それぞれに加わる電圧は \(R_8\)の抵抗と\(X_{C6}\)のリアクタンスと等しくなる。(抵抗の割合が等しいため)
よって、4Ωの電位差は、
$$V_4=V_8=16[V]$$
よって、有効電力は各抵抗で消費される電力であるため、
$$P=VI=\frac{(V_8)^2}{R_8}+\frac{(V_4)^2}{R_4}=\frac{16^2}{8}+\frac{16^2}{4}=96[W]$$
したがって、答えは(2)となる。
※以下参照

問10:過渡現象
問題
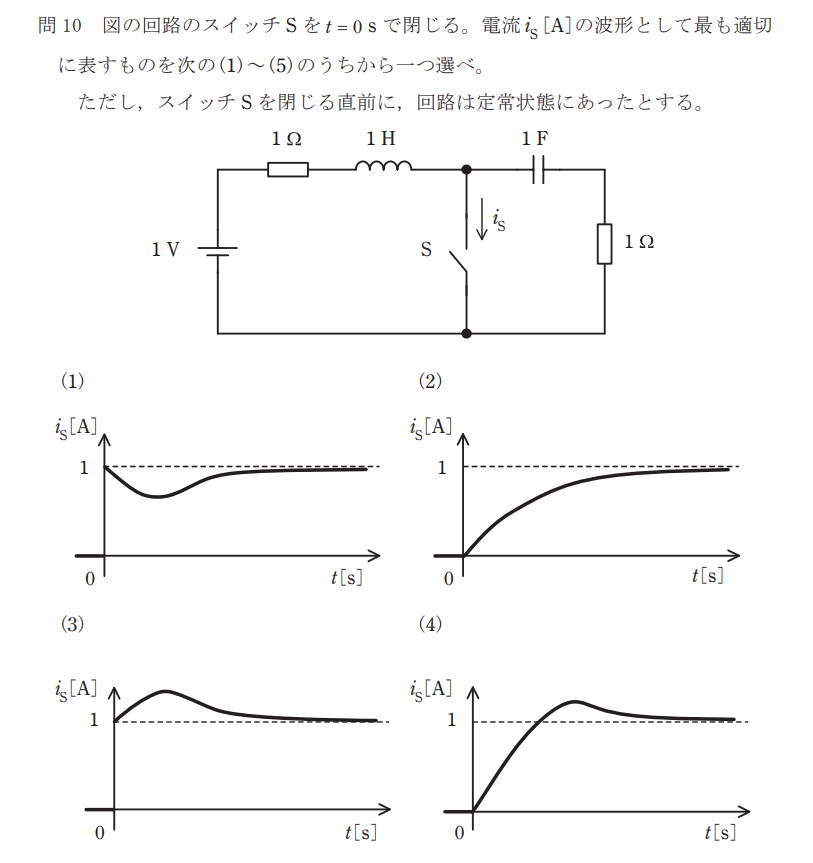
解説
コイルとコンデンサには以下の特性がある。
【コイル】※
初期値:開放状態
定常値:短絡状態
【コンデンサ】※
初期値:短絡状態
定常値:解放状態
スイッチSを閉じる前は、回路は定常状態であるため、コンデンサには十分な電荷が蓄えられている。
そのため、スイッチSを閉じると、電源→抵抗→コイル→電源という閉回路1と、コンデンサ→抵抗→コンデンサという閉回路2ができる。
閉回路1はコイルの特性から、初期値は電流が0で徐々に1に近づいていく。
閉回路にはコンデンサの特性から、初期値が電流がで徐々に0に近づいていく。
閉回路1と閉回路2に重ね合わせの理を適応すると、
答えは(5)となる。
※以下参照

問11:電子理論
問題

解説
(ア)可変容量ダイオードはpn結合に逆方向電圧※を加えて、空乏層を広げることで静電容量を調整する。
(イ)ダイオードの電圧・電流特性※
(ウ)レーザダイオードは順方向電圧※を掛けることで使用できる。
※以下参照

問12:電子理論
問題

解説
フレミングの左手の法則より、中指:電流の向き、人差し指:磁束密度の向き、親指:電磁力の向きで当てはめると、電磁力の向きが-y方向を向くことから、電荷は②の方向にローレンツ力が働く。
※負電荷であるため、電流の向きは指の方向とは逆方向になる。
よって、ローレンツ力の公式※より
$$F=evBcosφ$$
$$v=\frac{F}{eBcosφ}=\frac{1.0×10^{-8}}{-4.0×10^{-6}×1.0×10^{-3}×cos60°}=5.0[m/s]$$
したがって、答えは(5)となる。
※以下参照

問13:電子理論
問題
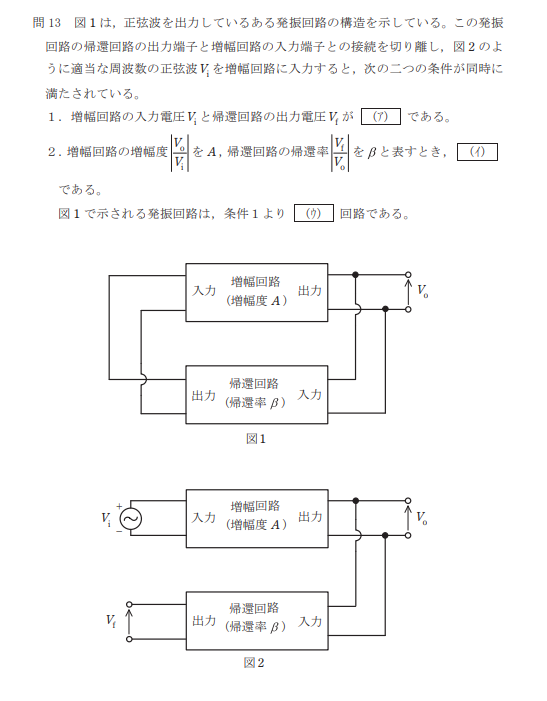

解説
(ア)発振回路を継続させるためには、増幅回路の入力電圧と帰還回路の出力電圧を同相にする必要がある。
(イ) 発振回路を継続させるためには、増幅回路の入力電圧≦帰還回路の出力電圧とする必要がある。(発信回路の振幅条件)
よって、
$$V_i≦V_f$$
$$V_i≦AβV_i$$
$$1≦Aβ$$
(ウ)図1の回路は出力にβを掛けたものをそのまま同相で入力しているため、正帰還回路となる。
したがって、答えは(1)となる。

問14:電気測定
問題

解説
(5):誤り
ディジタルオシロスコープで変化する電圧の波形を表示するのに、コンピュータで高速フーリエ変換 (FFT) を行う必要はない。

問15:三相交流回路
問題
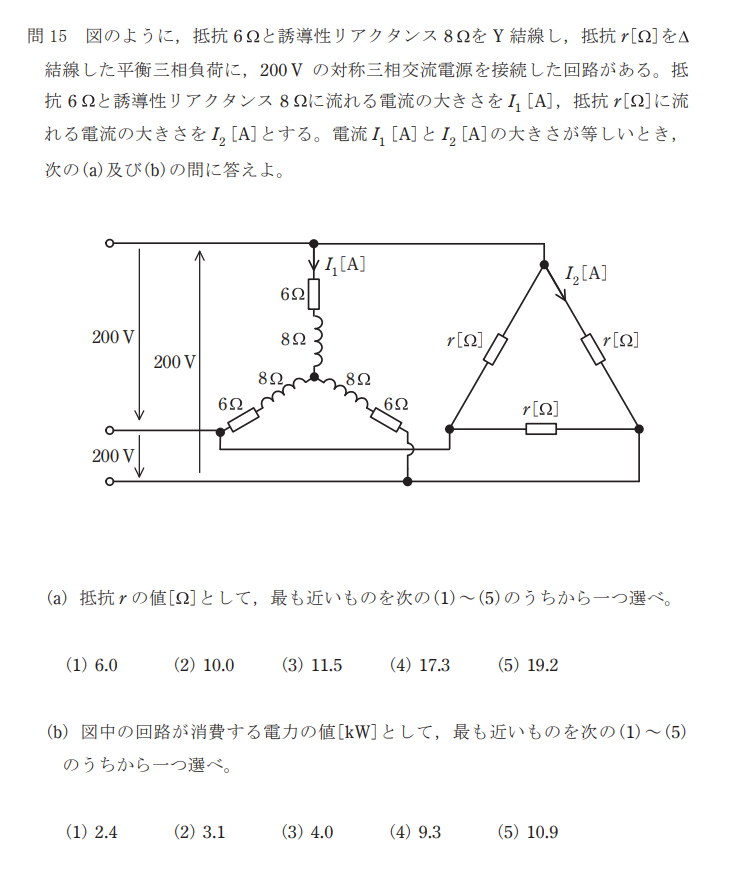
解説
抵抗6Ωと誘導性リアクタンス8Ωの合成インピーダンスは
$$Z=\sqrt{R^2+{X_L}^2}=\sqrt{6^2+8^2}=10[Ω]$$
また、線間電圧は以下のようになる。
$$V_1=\frac{200}{\sqrt{3}}[V]$$
よって、電流の大きさ\(I_1\)は、
$$I_1=\frac{V_1}{Z_1}=\frac{\frac{200}{\sqrt{3}}}{10}≒11.6[A]$$
また、題意より\(I_1=I_2\)であり、抵抗rに加わる電圧はΔ結線であるため200[V]となる。
よって、抵抗rは
$$r=\frac{200}{I_2}=\frac{200}{11.6}≒17.3[Ω]$$
したがって、(a)の答えは(4)となる。
また、回路が消費する電力の合計は、
$$P=6×{I_1}^2×3+r×{I_2}^2×3=6×{I_1}^2×3+r×{I_1}^2×3\\=6×{11.6}^2×3+17.3×{11.6}^2×3≒9330≒9.3[kW]$$
したがって、(b)の答えは(4)となる。

問16:電気測定
問題

解説
(a)直列回路の分流より,各電流計に流れる電流の比は抵抗の逆比となるから,
$$I_1:I_2=R_2:R_1$$
$$I_1:I_2=0.32:0.8$$
$$I_1:I_2=2:5$$
$$5I_1=2I_2$$
$$I_2=\frac{5}{2}I_2$$
よって、\(I_2\)は\(I_1\)の2.5倍になることから、先に最大目盛に達するのは\(A_2\)の電流計である。よって、\(I_2=100[A]\)の時、\(I_1=40[A]\)となるため、測定できる電流の最大値は140[A]となる。
したがって、答えは(5)となる。
(b) 二つの電流計を最大目盛にするためには,電流比 \(I_1\):\(I_2\) が1:2でなければならない。また、その時の抵抗値の比は 2:1 となる必要があるため,
$$R_1:(R_2+R)=2:1$$
$$R_1=2(R_2+R)$$
$$2=\frac{R_1}{R_2+R}$$
となる。よってRについて整理すると、
$$R=\frac{1}{2}R_1-R_2=\frac{1}{2}×0.8×10^{-3}-0.32×10-{-3}=8×10^{-5}[Ω]$$
したがって、答えは(3)となる。

問17:静電気
問題

解説
クーロンの法則より
$$F=k\frac{Q_AQ_B}{r^2}$$
$$k=\frac{Fr^2}{Q_AQ_B}=\frac{6×10^{-5}×{0.3}^2}{2×10^{-8}×3×10^{-8}}=9×10^9$$
したがって、答えは(4)となる。
\(Q_C\)を\(Q_A\)に接触させると、両導体球の電荷が平均化される。
$$Q’_A=Q’_C=\frac{Q_A}{2}=\frac{2×10^{-8}}{2}=1×10^{-8}[C]$$
次に\(Q_C\)を\(Q_B\)に接触させると、
$$Q’_B=Q’_C=\frac{Q_B+Q’_A}{2}=\frac{3×10^{-8}+1×10^{-8}}{2}=2×10^{-8}[C]$$
次に導体球Aと導体球Cの距離を\(r_{AC}\)とする。
導体球Cの受ける力が釣り合うため、次の式が成り立つ。
$$F=k\frac{Q’_AQ’_C}{r^2_{AC}}= k\frac{Q’_BQ’_C}{{r-r^2_{AC}}}$$
$$\frac{Q’_A}{r’^2}=\frac{Q’_B}{{r-r_{AC}}}$$
$$r^2_{AC}+0.6r_{AC}-0.09=0$$
$$r_{AC}=0.124[m]$$
したがって、答えは(4)となる。

問18:電子理論
問題
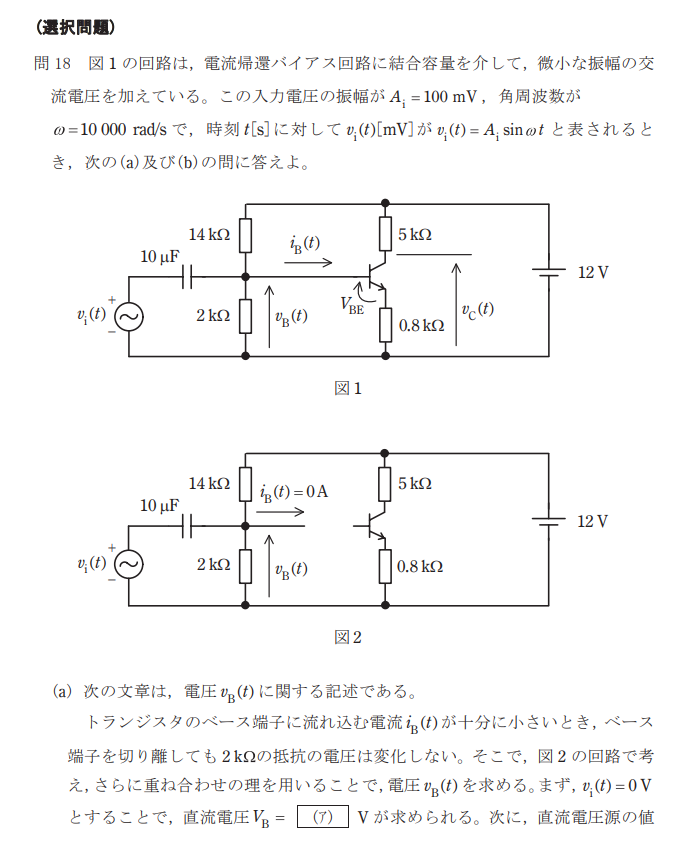

解説
(a)
(ア)次の閉回路に分圧の式を適応すると、
$$v_B=V×\frac{2×10^3}{2×10^3+14×10^3}=12×\frac{2×10^3}{2×10^3+14×10^3}=1.5[V]$$
(イ)コンデンサのインピーダンスが十分に小さく電圧降下がないと考えると、
交流電圧\(v_{B(t)}\)の振幅\(v_{i(t)}\)と同じ大きさの振幅 AB=100 [mV] が現れることになる。
(ウ) コンデンサのインピーダンスが十分に小さく電圧降下がないと考えると、
\(v_{B(t)}\)は \(v_{i(t)}\)と等しくなるので,位相差はなく \(θ_B\)=0[rad]と求められる。
したがって、答えは(4)となる。
(b)
(a)より, \(v_{B(t)}=1.5+0.1sinωt[V]\) であり,ベース・エミッタ間電圧は 0.7 V であるから,エミッタ電圧 \(v_{E(t)}\)[V] は,
$$v_{E(t)}=v_{B(t)}−0.7=1.5+0.1sinωt−0.7=0.8+0.1sinωt [V]$$
となる。よって,エミッタ電流\(i_{E(t)}\)[A] は,
$$i_{E(t)}=\frac{vE(t)}{0.8×10^3}=\frac{0.8+0.1sinωt}{0.8×10^3}=(1.0+0.125sinωt)×10^{−3}[A]$$
となり,ベース電流が十分に小さいとすれば,コレクタ電流は i_{C(t)}[A] は,
$$i_{C(t)}≒i_{C(t)}=(1.0+0.125sinωt)×10^{−3 }[A]$$
となる。よって,コレクタ電圧v_{C(t)}[V] は,
$$v_{C(t)}=12−5×10^3×i_{C(t)}=12−5×10^3×(1.0+0.125sinωt)×10^{−3}\\=12−5−0.625sinωt=7−0.625sinωt=7+0.625sin(ωt+π) [V]$$
したがって、答えは(4)となる。


