理論その4 交流回路(Alternating Current)

このページでは、交流回路の公式や重要単語とその解説について掲載しています。
また、その公式がどの過去問に使われているかについても記載しています。
交流回路の分野では、リアクタンスを含んだ交流回路の計算や力率の計算問題が中心に出題されます。
ベクトル図や複素数を用いた計算には慣れが必要であるため、繰返し計算問題を解く必要があります。
周期と周波数
周期は、周波数の逆数である。
$$\Large{T = \frac {1}{f}}$$
\(T\):周期[s] \(f\):周波数[Hz]
角周波数
角周波数は、周波数に比例する。
$$\Large{ω = 2πf}$$
\(ω\):角周波数[rad/s] \(f\):周波数[Hz]
交流の瞬時値
瞬時値は、それぞれの時刻における値を表す。
電圧
$$\Large{e = \sqrt{2}Esin(ωt+Φ)}$$
\(e\):交流電圧の瞬時値[V] \(E\):交流電圧の実効値[V] \(ω\):各周波数[rad/s] \(t\):時間[s] \(Φ\):初期位相[rad]
電流
$$\Large{i = \sqrt{2}Isin(ωt+Φ)}$$
\(i\):交流電流の瞬時値[A] \(I\):交流電流の実効値[V] \(ω\):各周波数[rad/s] \(t\):時間[s] \(Φ\):初期位相[rad]
交流電圧の平均値
最大値に\(\frac{2}{π}\)を掛けた値が実効値となる。
$$\Large{V_{avg} = \frac {2}{π}E_m}$$
\(V_{avg}\):交流電圧の平均値[V] \(E_m\):交流電圧の最大値[V]
交流電圧の実効値
最大値を\(\sqrt{2}\)で割った値が実効値となる。
$$\Large{V = \frac {1}{\sqrt{2}}E_m}$$
\(V\):交流電圧の実効値[V] \(E_m\):交流電圧の最大値[V]
直交座標 ⇒ 極座標
$$\Large{\vec{E} = {(x,y)}}$$
$$\Large{\Downarrow}$$
$$\Large{\vec {E} = \sqrt{x^2+y^2}\angle \tan^{-1} \frac {y}{x}}$$
極座標 ⇒ 直交座標
$$\Large{\vec {E} = E\angleΦ}$$
$$\Large{\Downarrow}$$
$$\Large{\vec {E} = (EcosΦ,EsinΦ)}$$
瞬時値 ⇒ 極座標
$$\Large{e = \sqrt{2}Esin(ωt+Φ)}$$
$$\Large{\Downarrow}$$
$$\Large{\vec {E} =E\angleΦ}$$
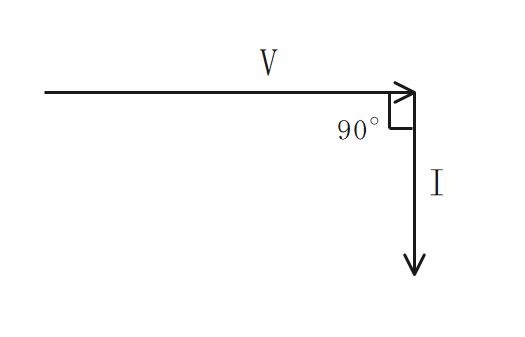
誘導性リアクタンス
誘導性リアクタンスは、周波数とインダクタンスの積に比例する。
Lのみの回路では、IはVに対し、\(\boldsymbol{\frac{π}{2}}\)[rad]遅れる
$$\Large{X_L = ωL = 2πfL}$$
\(X_L\):誘導性リアクタンス[Ω] \(ω\):各周波数[rad/s] \(L\):インダクタンス[H] \(f\):周波数[Hz]
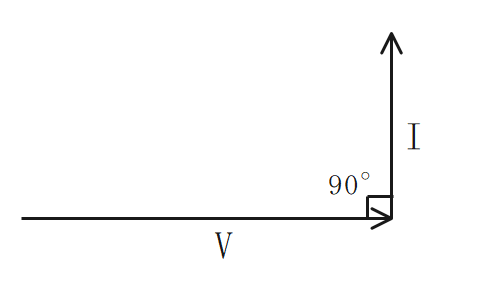
容量性リアクタンス
容量性リアクタンスは、周波数と静電容量の積に反比例する。
Cのみの回路では、IはVに対し、\(\boldsymbol{\frac{π}{2}}\)[rad]進む。
$$\Large{X_C = \frac {1}{ωC} = \frac {1}{2πfC}}$$
\(X_C\):容量性リアクタンス[Ω] \(ω\):各周波数[rad/s] \(C\):静電容量[F] \(f\):周波数[Hz]
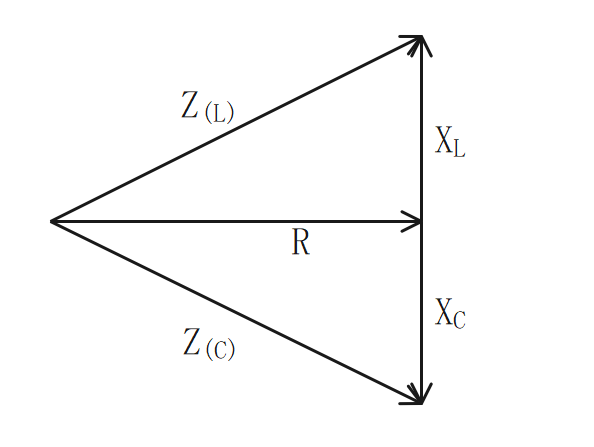
インピーダンス(直列回路)
インピーダンスは、抵抗とリアクタンスの合成からなる。
直列回路では電流が等しいため、電流ベクトルを基準にする。
R-L直列回路
$$\Large{Z = \frac {V}{I} = \sqrt{R^2+X^2_L}}$$
\(Z\):インピーダンス[Ω] \(V\):電圧[V] \(I\):電流[A] \(R\):抵抗[Ω] \(X_L\):誘導性リアクタンス[Ω]
R-C直列回路
$$\Large{Z = \frac {V}{I} = \sqrt{R^2+X^2_C}}$$
\(Z\):インピーダンス[Ω] \(V\):電圧[V] \(I\):電流[A] \(R\):抵抗[Ω] \(X_C\):容量性リアクタンス[Ω]
R-L-C直列回路
$$Z = \frac {V}{I} = \sqrt{R^2+{(X_L-X_C)}^2}$$
\(Z\):インピーダンス[Ω] \(V\):電圧[V] \(I\):電流[A] \(R\):抵抗[Ω] \(X_L\):誘導性リアクタンス[Ω] \(X_C\):容量性リアクタンス[Ω]
アドミタンス(並列回路)
アドミタンスは、抵抗とリアクタンスの逆数の合成からなる。
並列回路では電圧が等しいため、電圧ベクトルを基準にする。
並列回路の電流
$$\Large{I = \frac {V}{Z} = VY}$$
\(I\):電流[A] \(Z\):インピーダンス[Ω] \(V\):電圧[V] \(Y\):アドミタンス[S]
R-L並列回路
$$\Large{Y = \sqrt{(\frac{1}{R})^2 + (\frac{1}{X_L})^2}}$$
\(Y\):アドミタンス[S] \(R\):抵抗[Ω] \(X_L\):誘導性リアクタンス[Ω]
R-C並列回路
$$\Large{Y = \sqrt{(\frac{1}{R})^2 + (\frac{1}{X_C})^2}}$$
\(Y\):アドミタンス[S] \(R\):抵抗[Ω] \(X_C\):容量性リアクタンス[Ω]
R-L-C並列回路
$$\Large{Y = \sqrt{(\frac{1}{R})^2 + ({\frac{1}{X_L}-\frac{1}{X_C}})^2}}$$
\(Y\):アドミタンス[S] \(R\):抵抗[Ω] \(X_L\):誘導性リアクタンス[Ω] \(X_C\):容量性リアクタンス[Ω]
共振
誘導性リアクタンスXL=容量性リアクタンスXCの時を、共振状態という。
共振周波数
共振状態の時の周波数fを共振周波数f0という。
$$\Large{f_0 = \frac {1}{2π\sqrt{LC}}}$$
\(f_0\):共振周波数[Hz] \(L\):インダクタンス[H] \(C\):静電容量[F]
以下、導出
$$X_L=X_C$$
$$2πf_0L=\frac{1}{2πf_0C}$$
$$f_0=\frac{1}{2π\sqrt{LC}}$$
直列共振回路
インピーダンスが最小\((Z=R)\)、電流は最大になる。
並列共振回路
インピーダンスが最大\((Z=∞\)、電流は最小になる。
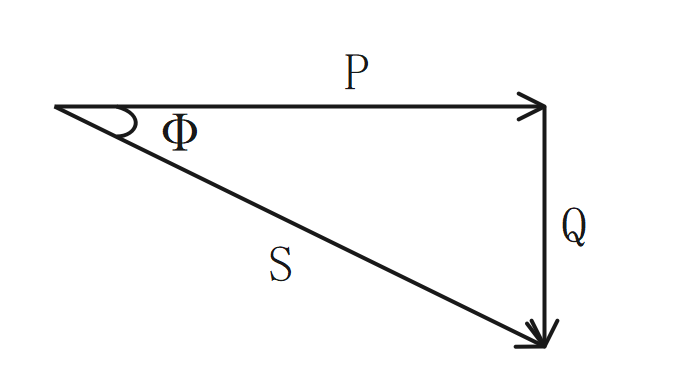
交流電力
皮相電力
$$\Large{S = VI = ZI^2}$$
\(S\):皮相電力[V・A] \(V\):電圧[V] \(I\):電流[A] \(Z\):インピーダンス[Ω]
有効電力
$$\Large{P = ScosΦ = RI^2}$$
\(P\):有効電力[W] \(S\):皮相電力[V・A] \(R\):抵抗[Ω] \(I\):電流[A]
無効電力
$$\Large{Q = SsinΦ = XI^2}$$
\(Q\):無効電力[var] \(S\):皮相電力[V・A] \(X\):リアクタンス[Ω] \(I\):電流[A]
交流電力の関係
$$\Large{S^2 = P^2 + Q^2}$$
\(S\):皮相電力[V・A] \(P\):有効電力[W] \(Q\):無効電力[var]
力率
皮相電力の大きさに対する有効電力の大きさの割合
$$\Large{cosΦ = \frac{P}{S} = \frac{R}{Z}}$$
\(cosΦ\):力率 \(P\):有効電力[W] \(S\):皮相電力[V・A] \(R\):抵抗[Ω] \(Z\):インピーダンス[Ω]
複素数を用いたインピーダンス計算
複素数表記にすると、オームの法則や分圧、分流など直流回路と同じように計算できるようになる。
抵抗と誘導性リアクタンス
$$\Large{Z = R+jX_L}$$
\(Z\):インピーダンス[Ω] \(R\):抵抗[Ω] \(X_L\):誘導性リアクタンス[Ω]
抵抗と容量性リアクタンス
$$\Large{Z = R-jX_C}$$
\(Z\):インピーダンス[Ω] \(R\):抵抗[Ω] \(X_C\):容量性リアクタンス[Ω]
抵抗と誘導性リアクタンスと容量性リアクタンス
$$\Large{Z = R+j(X_L-X_C)}$$
\(Z\):インピーダンス[Ω] \(R\):抵抗[Ω] \(X_L\):誘導性リアクタンス[Ω] \(X_C\):容量性リアクタンス[Ω]


