理論その8 電気測定(Electrical Measurements)

このページでは、電気測定の公式や重要単語とその解説について掲載しています。
また、その公式がどの過去問に使われているかについても記載しています。
電気計測の分野では、電気計器の特性を問う知識問題や分流器・倍率器を用いた回路の計算問題が中心に出題されます。
出題数はそれほど多くありませんが、比較的簡単な問題が多いため、点数を取りやすい分野になります。
誤差率
真値と測定値にどれだけの差があるかを表す。
$$\Large{ε = \frac {M-T}{T}×100}$$
\(ε\):誤差率[%] \(T\):真の値 \(M\):測定値
補正率
測定値を真値に近づけるために必要な量を表す。
$$\Large{α = \frac {T-M}{M}×100}$$
\(α\):補正率[%] \(M\):測定値 \(T\):真の値
電気計器
可動コイル形計器
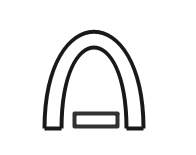
- 磁界中のコイルに電流を流した時に発生する電磁力を利用した計器。
・永久磁石を使用することで、磁束密度Bを一定にすることで、電流に比例したトルク(慣性モーメント)を得ることができる。
・慣性モーメントにより、指針は平均値を示す。
・直流用である。
・電圧計として使用する場合、倍率器を使う。
$$\Large{T = FD = BlID}$$
\(T\):トルク[Nm] \(F\):力[N] \(D\):腕の長さ \(B\):磁束密度[T] \(l\):導体の長さ[m] \(I\):電流の大きさ[A]
整流形計器
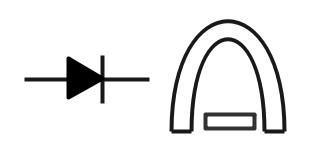
- 可動コイル形計器に整流器を取り付けた計器。
・感度が良い。
・指示値は実効値を示す。
・交流用である。
・ひずみ波を測定すると誤差は大きくなる。
・入力された信号の平均値×波形率を表示する。
なお、正弦波交流において波形率は1.11である。
熱電対形計器
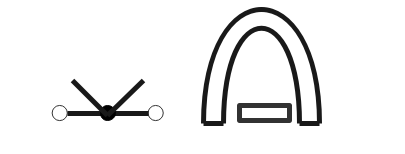
- 異なる2種類の金属を接合し、一方を加熱したときの温度と他方の金属との温度差によって、起電力が発生し電流が流れるのを利用した計器。(ゼーベック効果)。
・高周波数の測定ができる。
・指示値は実効値を示す。
・直流と交流の両方に利用できる。
可動鉄片形計器
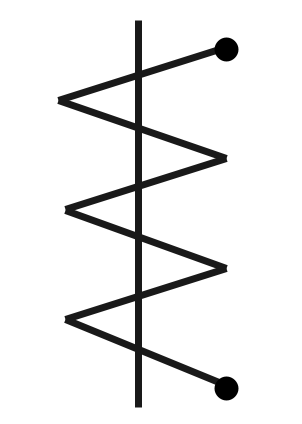
- 固定コイル中に2つの鉄片を同じ向きで配置する。固定コイルに電流が流れると磁界が発生し、同一方向に磁化された鉄心に反発力(駆動トルク)が生じる。この駆動トルクの大きさによって指針が変化する計器。
・駆動トルクは電流の2乗に比例する。
・50Hz、60Hzの商用周波数で広く使われている。
・指示値は実効値を示す。
・一般に交流用として使われる。
電流力計形計器
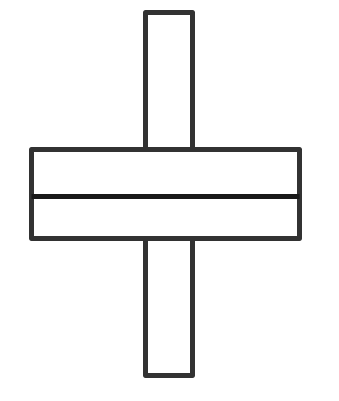
- 2つの固定コイルと1つの可動コイルに電流を流すと、それぞれのコイルに磁界が発生する。
それぞれのコイルに反発力が働くようにコイルを配置すると、電流の大きさを測定できる。
・指針の振れ角は負荷電力に比例する。(P=VIcosΦ)
・指示値は実効値を示す。
・直流と交流の両方に利用できる。
・一般に電力の測定に用いられる。
静電形計器
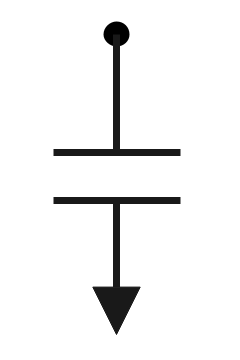
- 電極板間に測定したい電圧を加えると、電極板に電荷が蓄えられ、静電力が生じる。この静電力を利用した計器。
・低い電圧では駆動トルクが小さく誤差が大きくなるため、高電圧測定用の電圧計として用いられる。
・指示値は実効値を示す。
・直流と交流の両方に利用できる。
誘導形電力量計
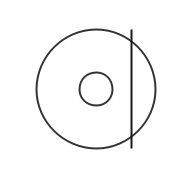
- アラゴの円板の原理を利用した計器。
・交流の電力量を測定するのによく使われる。
$$\Large{N=KPT}$$
\(N\):回転数[rpm] \(K\):計器定数 \(P\):電力[kW] \(T\):時間[h]
分流器
- 電流計に並列に接続した抵抗器。
- 並列の分流作用を用いて、電流計の測定範囲を超えた電流を測定したい場合に利用する。
抵抗値
$$\Large{R_S = \frac{r_a}{m-1}}$$
\(r_a\):電流計の内部抵抗[Ω] \(m\):倍率
倍率
- 電流計の測定上限の何倍まで測定できるかを表す。
$$\Large{m = \frac{I}{I_a}}$$
\(I\):全体の電流[A] \(I_a\):電流計に流れる電流[A]
倍率器
- 電圧計に直列に接続した抵抗器。
- 直列の分圧作用を用いて、電圧計の測定範囲を超えた電圧を測定したい場合に利用する。
抵抗値
$$\Large{R_m = r_v(m-1)}$$
\(r_v\):電圧計の内部抵抗[Ω] \(m\):倍率
倍率
- 電圧計の測定上限の何倍まで測定できるかを表す。
$$\Large{m = \frac{V}{V_v}}$$
\(V\):全体の電圧[V] \(V_v\):電圧計に加わる電圧[V]
抵抗の測定法
電圧降下法
- 抵抗による電圧降下と電流を測定し、オームの法則により抵抗値を算出する。
・低精度である。
ホイートストンブリッジ回路による測定
- ブリッジの平衡条件を用いて、抵抗値を算出する。
・高精度である。
電力の測定法
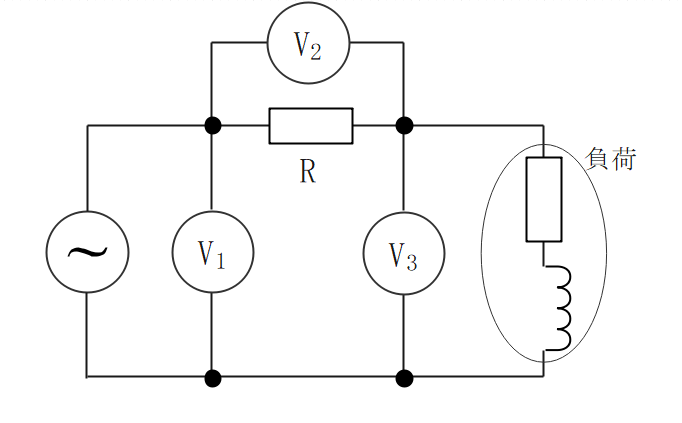
三電圧計法
- 電圧計3つと抵抗1つで負荷が消費する電力の計算を行う。
※単相交流のみ測定可
$$P = \frac{1}{2R}((V_1)^2-(V_2)^2-(V_3)^2)$$
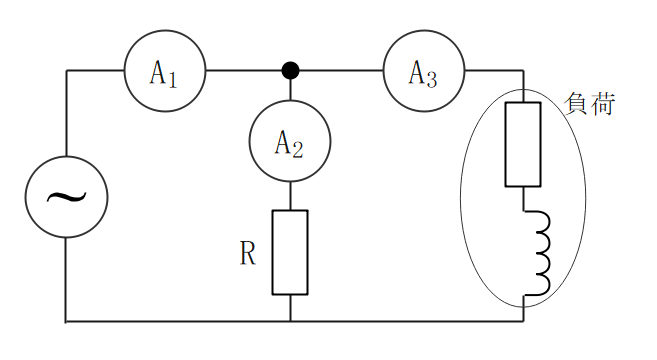
三電流計法
- 電流計3つと抵抗1つで負荷が消費する電力の計算を行う。
※単相交流のみ測定可
$$P = \frac{R}{2}((I_1)^2-(I_2)^2-(I_3)^2)$$
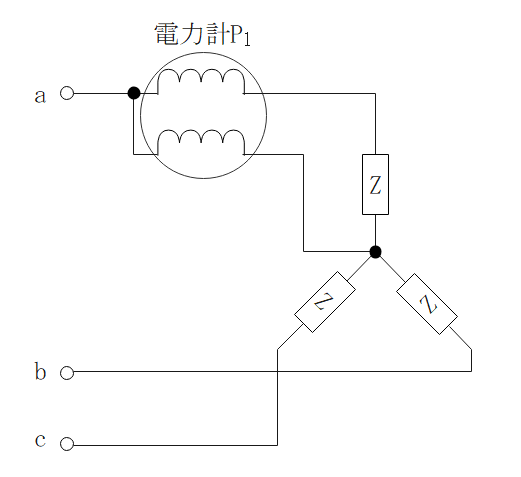
一電力計法
- 1相分の電力を測定して、3倍することで電力を求める。
・負荷が3相とも等しいとき(平衡状態)に使える。
・Y結線のときのみ使える。
・電流計3つと抵抗1つで負荷が消費する電力の計算を行う。
$$\Large{P = 3P_1}$$
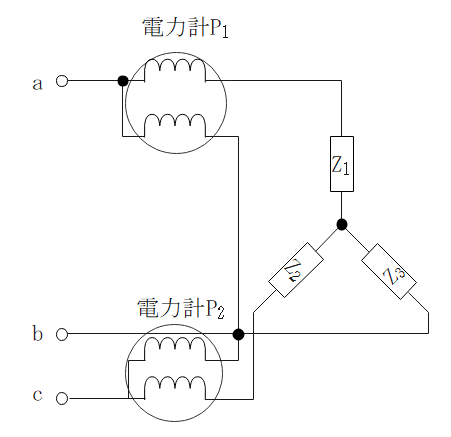
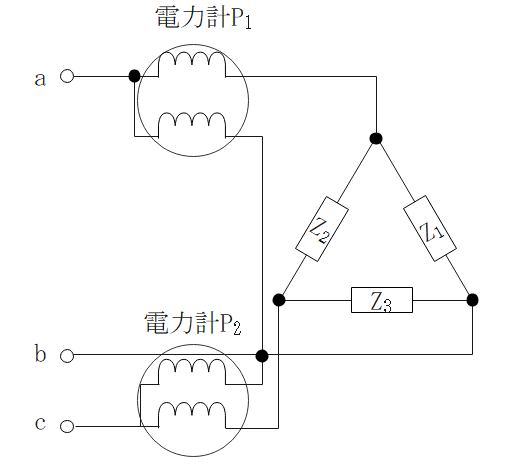
二電力計法
- 2相分の電力を測定し、合計することで全体の電力を求める。
・負荷が不平衡状態でも使える。
・Δ、Y結線の両方とも使える。
・負荷の力率によっては、電力系の指針が逆に振れることがある。
$$\Large{P = P_1+P_2}$$
オシロスコープ
- 電気信号(電圧)の波形を表示する装置。
・縦軸:垂直感度(V/div) *電圧は瞬時
・横軸:掃引時間(s/div)
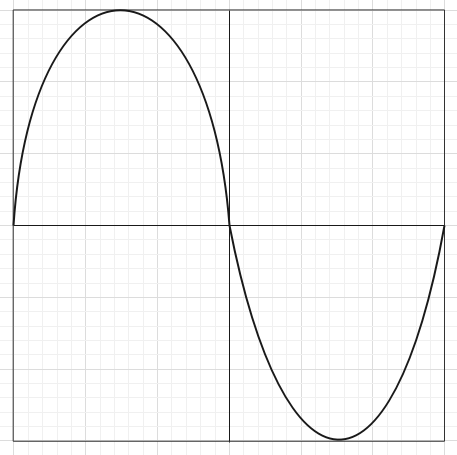
垂直偏向極板にのみ正弦波交流電圧を加えた場合
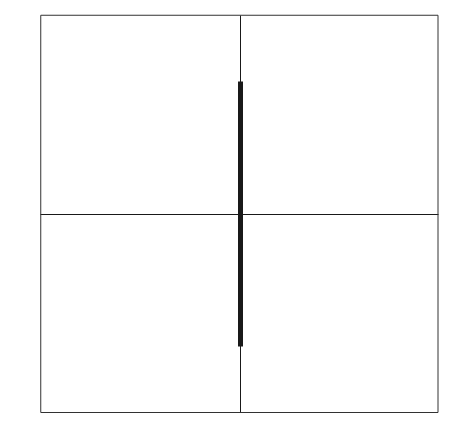
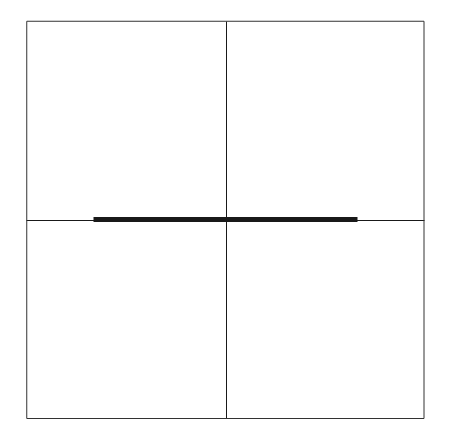
水平偏向極板にのみ正弦波交流電圧を加えた場合
計器の特性
アナログ計器
- 入力抵抗をできるだけ小さくする。
デジタル計器
- 入力抵抗をできるだけ大きくする。
- 二重積分形が用いられる。
データ変換
- アナログ量を忠実に再現するために必要な標本化の周期の上限は,再現したいアナログ量の最高周波数により決まる。
- 量子化において,一般には数値に誤差が生じる。
- 符号化では,量子化された数値が 2 進符号などのディジタル信号に変換される。
- ディジタル量は,伝送路の環境変化や伝送路で混入する雑音に強い。
- ディジタルオシロスコープで変化する電圧の波形を表示するには,その電圧をアナログ-ディジタル変換してからその結果を出力する。


