2022年下期 過去問 電力

このページでは、2022年下期電験三種試験の電力科目の解説を掲載しています。
問01:水力発電
問題

解説
(3)が誤り
日本における水力発電の発電電力量の比率は10%未満である。
※以下参照

問02:水力発電
問題

解説
衝動水車の説明。
比速度とは、落差1mで出力1kWを発生させたときの毎分の回転速度である。
答えは(5)となる。
※以下参照

問03:火力発電
問題

解説
(5)が誤り
コンパウンドサイクル発電の説明。
コンバインドサイクル発電は、大型補機が少なく一般の汽力発電に比べ所内率は小さい。
※以下参照

問04:原子力発電
問題

解説
原子力発電の特徴
答えは(1)となる。

※以下参照
問05:その他の発電
問題

解説
(5)が誤り
その他の発電方法の特徴
燃料電池発電は、発電時に振動や騒音は小さい。
※以下参照

問06:電力計算
問題

解説
パーセントインピーダンスの式より、
$$%Z=\frac{P_nZ}{{E_n}^2}×100=\frac{30×10^6×14.5}{{(66×10^3)}^2}≒9.99[Ω]$$
したがって、答えは(3)となる。
※以下参照

問07:変電所
問題

解説
変圧器の結線による特性の変化。
答えは(2)となる。
※以下参照

問08:送電
問題

解説
(2)が誤り。
トーショナルダンパは電線に取り付ける錘で,風による上下の振動を防止するためのものである。
※以下参照

問09:電力計算
問題

解説
受電端の三相電力の公式より、
$$P=\frac{V_SV_r}{X}sinδ$$
したがって、答えは(1)となる。
※以下参照

問10:地中電線
問題

解説
(3)が誤り。
(3)管路式は、他の方式と比較して熱放散が悪く,ケーブル条数が増加すると他のケーブルの温度上昇の影響を受けるため、さらに熱放散が悪くなり,送電容量が制限される。
※以下参照

問11:電気施設管理(法規)
問題

解説
文章に記載の通り。
(5)が答えとなる。
※以下参照

問12:配電
問題

解説
文章に記載の通り。
(3)が答えとなる。
※以下参照

問13:配電
問題

解説
(3)が誤り。
給電線のうちの一つに事故が発生しても,無停電で他の健全な給電線に供給系統を切り替え可能である。
※以下参照

問14:電気材料
問題

解説
文章の通り。
答えは(2)となる。
※以下参照

問15:火力発電
問題

解説
(a)
復水器で海水へ放出される熱量は、公式より
$$Q=qcρΔT=24×4.02×1.02×10^3×7≒688900≒6.89×10^5[kJ/s]$$
したがって、答えは(4)となる。
(b)
タービン室効率は次の公式で求められる。
$$η_T=\frac{P_T}{Q_i}$$
また、発電機効率からタービン軸出力を求めると、
$$η_G=\frac{P_G}{P_t}$$
$$P_T=\frac{P_G}{η_G}=\frac{600000}{0.98}≒612200[kW]$$
また、タービンに入る蒸気の熱量は、
$$Q_i=P_T+Q=612200+688900≒1301000[kJ/s]$$
よって、タービン室効率は、
$$η_T=\frac{612200}{1301000}≒0.4706≒47.1[%]$$
したがって、答えは(3)となる。
※以下参照

問16:電力計算(未完)
問題

解説
(a)
題意に沿って単線図を描くと図5のようになり,各値を図5のようにおく。力率 cosθ=0.8 であるから,
$$sinθ=\sqrt{1-cos^2θ}=\sqrt{1-0.8^2}=0.6$$
であり,受電端電圧\(V_r \)[V] 基準の電圧降下率 \(\frac{ε}{V_r}\)が10%であるから,送電可能な電流値 I [A] は,
$$\frac{ε}{V_r}=\frac{\sqrt{3}I(Rcosθ+Xsinθ)}{V_r}$$
$$0.1=\frac{\sqrt{3}I(6×0.8+4×0.6)}{60×10^3}$$
$$I≒481.1[A]$$
となる。よって,受電可能な皮相電力 S [MV⋅A] は,
$$S=\sqrt{3}V_rI=\sqrt{3}×60×10^3×481.1=50×10^6$$
したがって、答えは(3)となる。
※\(sin^2θ+cos^2θ=1 → sinθ=\sqrt{1-cos^2θ}=\sqrt{1-0.64}=0.6\)
(b)
$$sinθ=\sqrt{1-cos^2θ’}=\sqrt{1-0.6^2}=0.8$$
$$P’=S’cosθ’=65×0.6=39[MW]$$
$$Q’=S’sinθ’=65×0.8=52[Mvar]$$
受電端電圧基準の電圧降下率は、
$$\frac{ε}{V_r}=\frac{\sqrt{3}I(Rcosθ+Xsinθ)}{V_r}$$
であり、
$$P’=\sqrt{3}V_rI’cosθ’$$
$$ I’cosθ’= \frac{P’}{\sqrt{3}V_r}$$
$$Q’=\sqrt{3}V_rI’sinθ’$$
$$ I’sinθ’= \frac{Q’}{\sqrt{3}V_r}$$
であるため、
$$\frac{ε}{V_r}=\frac{\sqrt{3}I‘(Rcosθ’+Xsinθ’)}{V_r}=\frac{RP’+XQ’}{{V_r}^2}$$
と変形できる。ここで,調相設備から無効電力 \(Q_C\) [Mvar] を接続したときに電圧降下率が 10 % に維持されたとなっていることから,
$$0.1=\frac{RP’+X(Q’-Q_C)}{{V_r}^2}=\frac{6×39×10^6+4×(52×10^6-Q_C)}{{60×10^3}^2}$$
$$Q_C=20.5×10^6[var]$$
したがって、答えは(2)となる。
※以下参照

問17:線路計算(未完)
問題
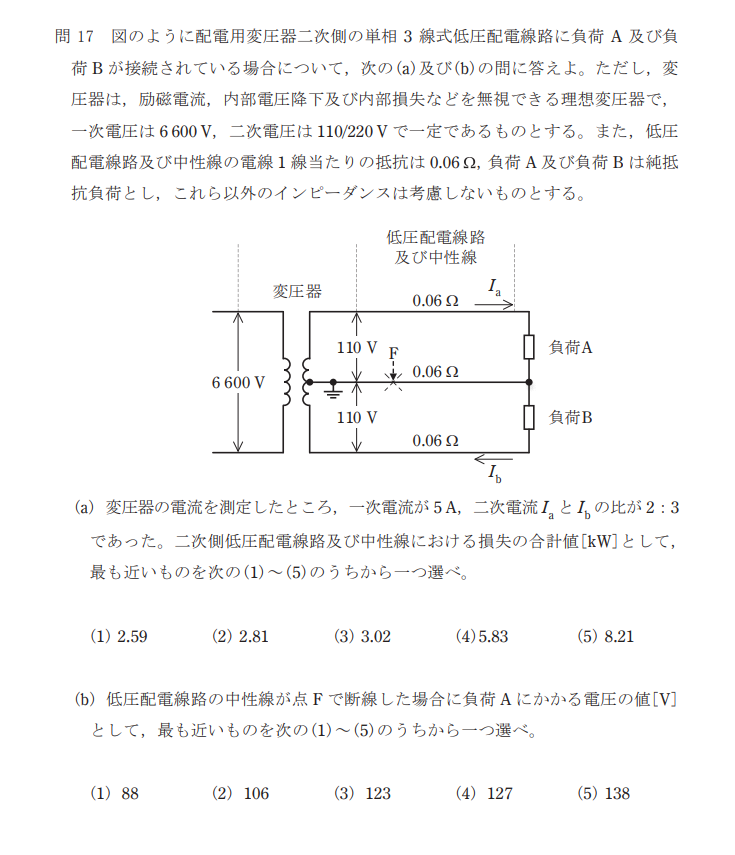
解説

※以下参照

