2022年上期 過去問 理論

このページでは、2022年上期電験三種試験の理論科目の解説を掲載しています。
問01:静電気
問題

解説
(1)正しい。
平行板コンデンサ内(誘電体内)は電界が一様に発生しているため,平行板コンデンサ内(誘電体内)の等電位面は電極板と平行になる。
(2)正しい。
電荷量の式は\(Q=CV\)。静電容量の式は\(C=\frac{εA}{l}\)
Qの式にCを代入すると、\(Q=\frac{εA}{l}V\)となる。
(3)誤り。
平行平板コンデンサの電界と電位の関係式は以下の通りである。
$$E=\frac{V}{l}$$
よって、電界の大きさに誘電率は影響しない。
(4)正しい。
コンデンサに蓄えられる電荷の式より
$$Q=DA$$
$$D=\frac{Q}{A}$$
よって、電束密度は単位面積当たりの電荷量の大きさに等しい。
(5)正しい。
静電エネルギーは\(W=\frac{1}{2}CV^2\)で求められる。ここで\(C=\frac{εA}{l}\)を代入すると、\(W=\frac{1}{2}\frac{εA}{l}V^2\)となる。
よって、静電エネルギーの大きさは電極板の面積に比例する。
※以下参照

問02:静電気
問題
解説
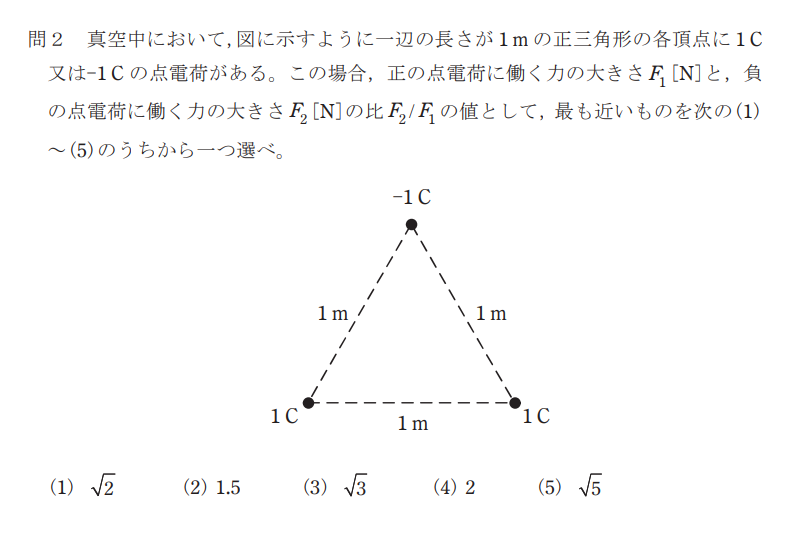
各電荷間に加わる力の大きさは、クーロンの法則より
$$F=\frac{Q_1Q_2}{4πεr^2}=\frac{1×1}{4πε1^2}=\frac{1}{4πε}$$
図1より, 1 [C] の電荷に加わる力は F [N] と等しいため,
$$F_1=F[N]$$
となる。
また, −1 [C] の電荷に加わる力は正三角形の性質より,
$$F_2=\frac{\sqrt{3}}{2}F×2=\sqrt{3}F[N]$$
よって、\(F_1\)と\(F_2\)の比は、
$$\frac{F_2}{F_1}=\frac{\sqrt{3}F}{F}=\sqrt{3}$$
したがって、答えは(3)となる。
※以下参照

問03:電磁気
問題
解説
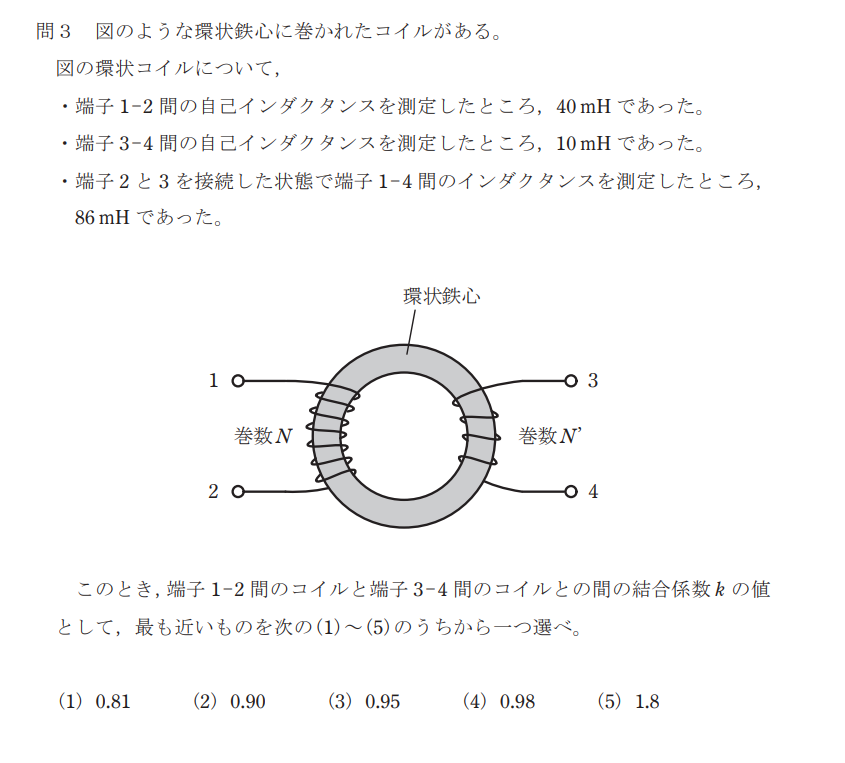
端子 1−2 間の自己インダクタンスを \(L_{12}=40\)[mH] ,端子 3−4 間の自己インダクタンスを \(L_{34}=10\) [mH] とおくと、
相互インダクタンス M は
$$M=k\sqrt{L_{12}L_{34}}=k\sqrt{40×10}=20k[mH]$$
端子 2 と 3 を接続した状態は和動接続となるため,合成インダクタンス \(L_0\)は
$$L_0=L_{12}+L_{34}+2M$$
各値を代入すると、
$$86=40+10+20k$$
よって、
$$k=0.90$$
したがって、答えは(2)となる。
※以下参照

問04:電磁気
問題
解説
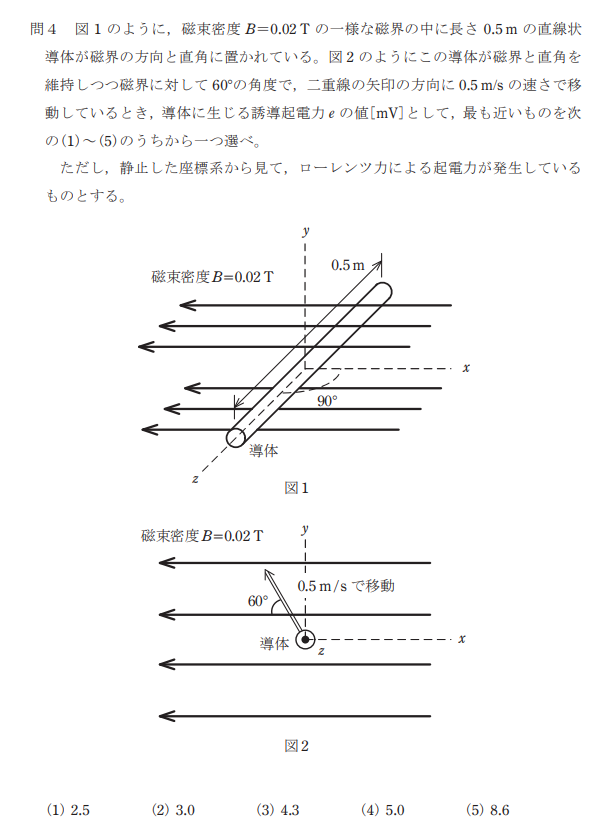
導体の速度の大きさを\(v[m/s]\)とすると,
$$v=0.5sin60°=0.5×\frac{\sqrt{3}}{2}≒0.4330[m/s]$$
よって、誘導起電力の大きさは、
$$e=Blvsinθ=0.02×0.5×0.4330×sin90°=0.00433[V]≒4.3[mV]$$
したがって、答えは(3)となる。
※以下参照

問05:直流回路
問題
解説
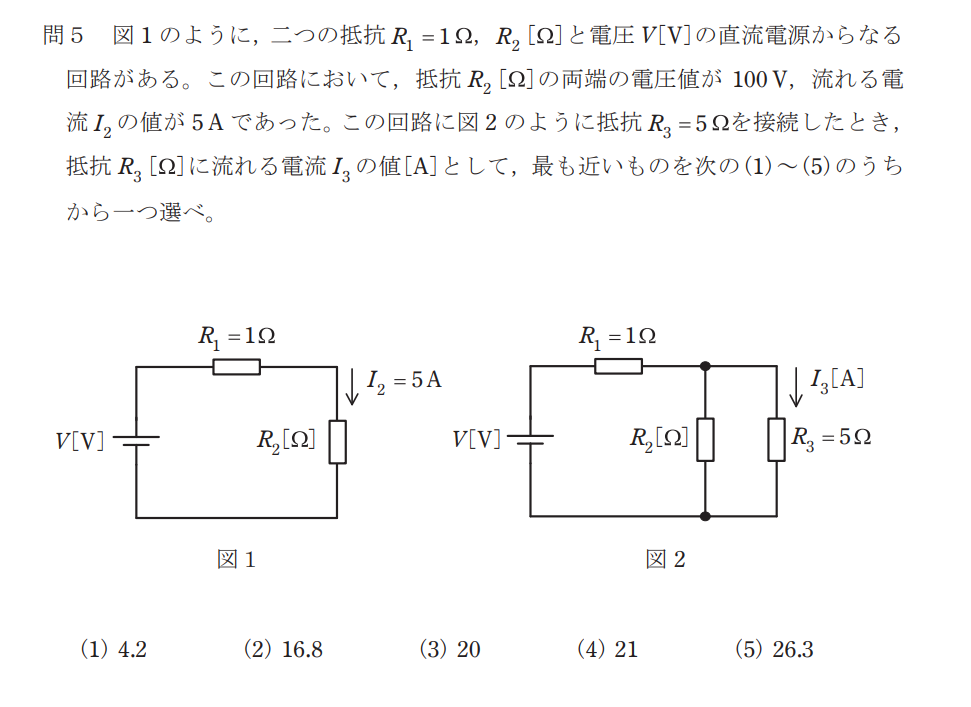
問題文から、\(R_2\)は
$$R_2=\frac{100}{I_2}=\frac{100}{5}=20[Ω]$$
また、\(R_1\)の両端の電圧値は、
$$V_1=R_1I_2=1×5=5[V]$$
よって、電源電圧は
$$V=V_1+100=5+100=105[V]$$
次に図2の合成抵抗を求めると、
$$R_O=R_1+\frac{R_2R_3}{R_2+R_3}=1+\frac{20×5}{20+5}=5[Ω]$$
よって、回路内の全電流は
$$I_O=\frac{V}{R_O}=\frac{105}{5}=21[A]$$
よって、\(I_3\)は並列回路の分流より、
$$I_3=I×\frac{R_2}{R_2+R_3}=21×\frac{20}{20+5}=16.8[A]$$
したがって、答えは(2)となる。
※以下参照

問06:静電気
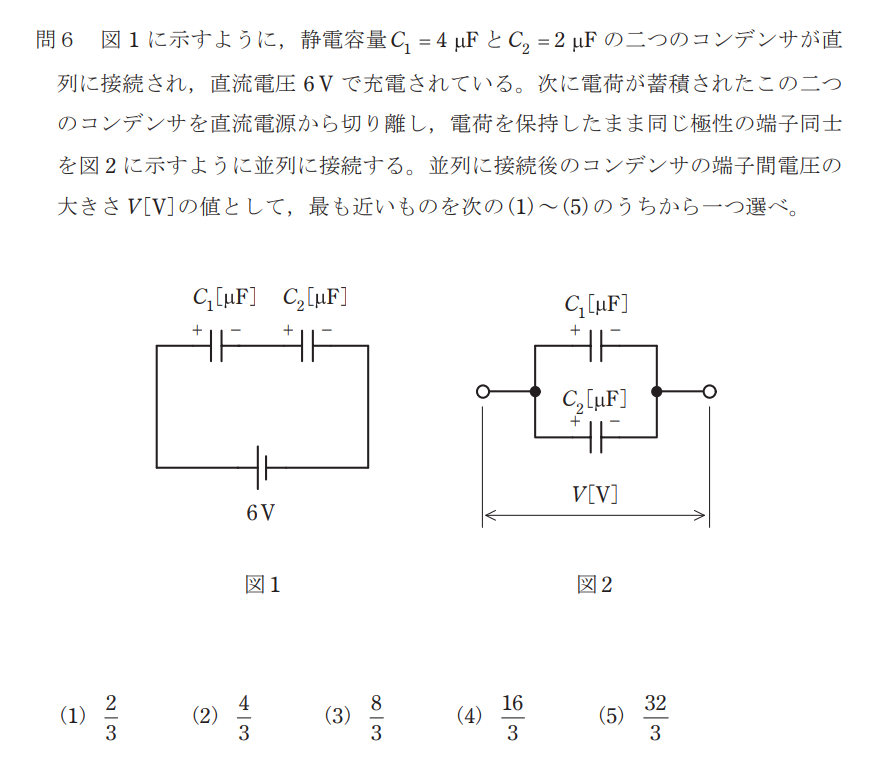
問題
解説
図1より合成静電容量は、
$$C_{O1}=\frac{C_1C_2}{C_1+C_2}=\frac{4×2}{4+2}=\frac{4}{3}[μF]$$
よって、全電荷量は、
$$Q_1=C_{O1}V=\frac{4}{3}×6=8[μC]$$
次に図2の合成静電容量は、
$$C_{O2}=C_1+C_2=4+2=6[μF]$$
また、全電荷量は、
$$Q_2=2×Q_1=2×8=16[μC]$$
よって、電源電圧は、
$$$V=\frac{Q_2}{C_{O2}}=\frac{16}{6}=\frac{8}{3}$$
したがって、答えは(3)となる。
※以下参照

問07:直流回路(作成中)(ここから未反映)
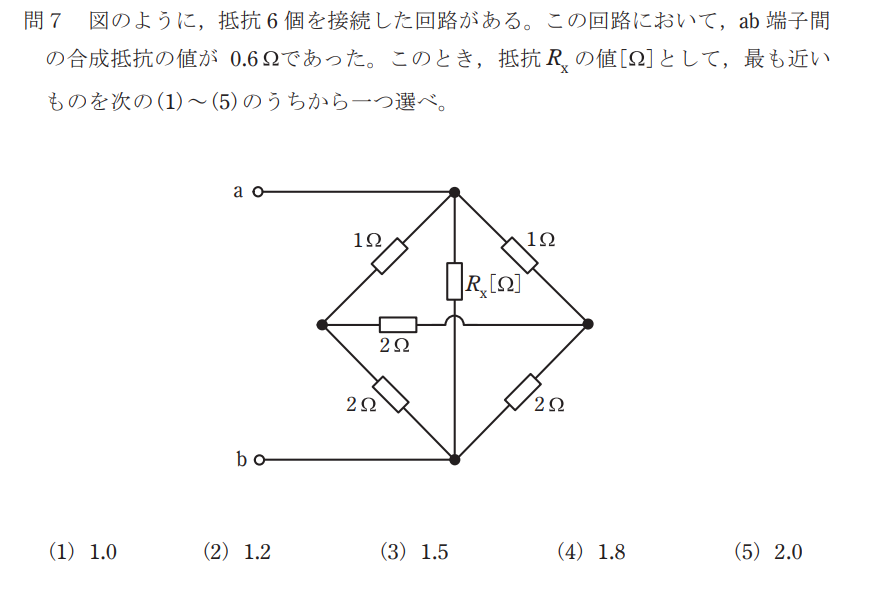
問題
解説
2Ωの抵抗3つをΔ-Y変換すると、各抵抗値は
$$R=\frac{2×2}{2+2+2}=\frac{2}{3}$$
よって、回路右部の合成抵抗は、
$$R’=\frac{2}{3}+\frac{{(1+\frac{2}{3})}{(1+\frac{2}{3})}}{{1+\frac{2}{3}}+{1+\frac{2}{3}}}=\frac{3}{2}$$
よって、並列回路の合成抵抗より、
$$\frac{1}{R_O}=\frac{1}{R_x}+\frac{1}{R’}$$
$$\frac{1}{0.6}=\frac{1}{R_x}+\frac{1}{\frac{3}{2}}$$
$$R_x=1[Ω]$$
したがって、答えは(1)となる。
※以下参照

問08:交流回路
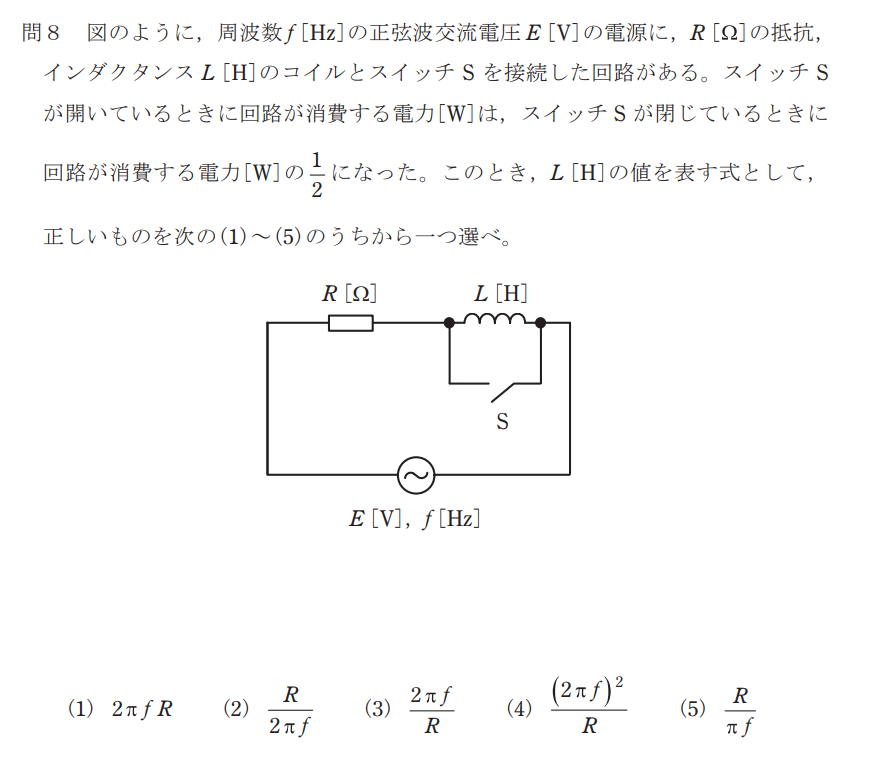
問題
解説
スイッチが閉じているときの全電流は
$$I_1=\frac{E}{R}$$
スイッチが開いているときの全電流は
$$I_2=\frac{E}{R+jX_L}$$=\frac{E}{R+j2πfL}$$
となり、その大きさは、
$$I_1=\frac{E}{R}$$
$$I_2=\frac{E}{\sqrt{R^2+{j2πfL}^2}}$$
回路が消費する電力は、\(P=RI^2\)より求められる。
したがって、
$$P_2=\frac{1}{2}P_1$$
$$R{I_2}^2=\frac{1}{2}R{I_1}^2$$
$$I_2=\frac{1}{\sqrt{2}}I_1$$
$$I_1=\sqrt{2}I_2$$
$$\frac{E}{R}=\sqrt{2}×\frac{E}{\sqrt{R^2+{j2πfL}^2}}$$
$$L=\frac{R}{2πf}$$
したがって、答えは(2)となる。
※以下参照

問09:交流回路
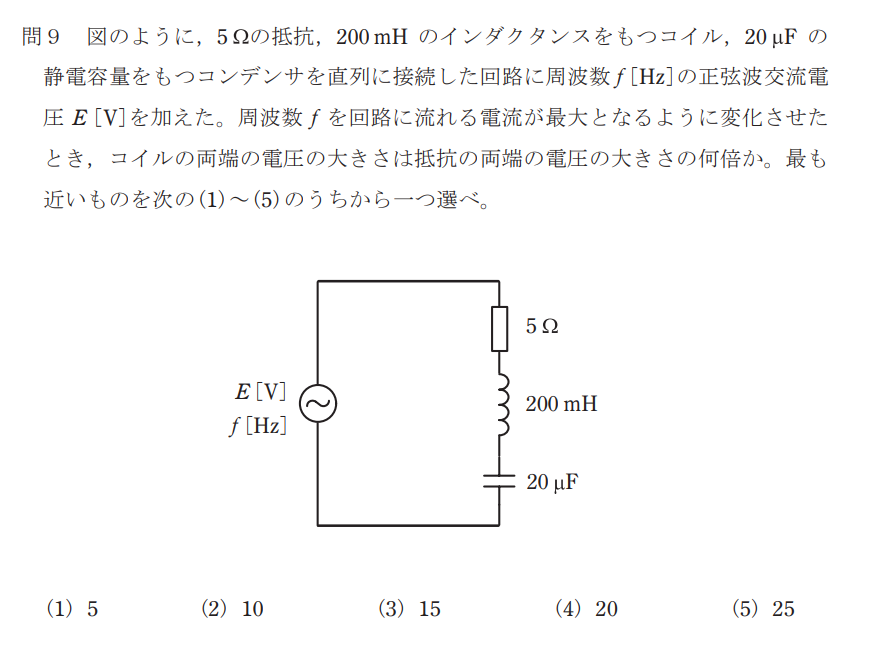
問題
解説
「周波数fを回路に流れる電流が最大となるように変化」とあることから、fは共進周波数であることがわかる。
よって、
$$f_O=\frac{1}{2π\sqrt{LC}}= \frac{1}{2π\sqrt{200×10^{-3}×20×10^{-6}}}=\frac{250}{π}[Hz]$$
となる。
この時のコイルとコンデンサのリアクタンスは、
$$X_L=2πfL=2π\frac{250}{π}L=2π\frac{250}{π}×200×10^{-3}=100[Ω]$$
$$X_C=2πfC=\frac{2π\frac{250}{π}}{C}=\frac{2π\frac{250}{π}}{200×10^{-6}}=100[Ω]$$
よって、コイルと抵抗の両端の電圧の比は、
$$\frac{V_L}{V_R}=\frac{X_LI}{RI}=\frac{X_L}{R}=\frac{100}{5}=20$$
したがって、答えは(4)となる。
※以下参照

問10:交流回路
問題
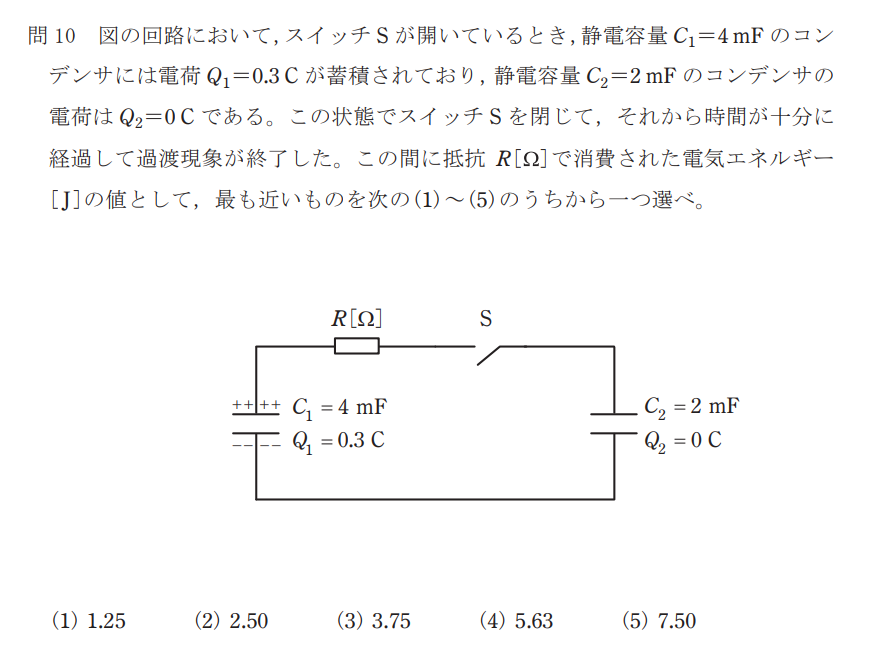
解説
スイッチSが開いているとき、C1のコンデンサに蓄えられている静電エネルギーは、
$$W_1=\frac{1}{2}CV^2=\frac{{Q_1}^2}{2C_1}=\frac{{0.3}^2}{2×40×10^(-3)}=11.25[J]$$
スイッチを閉じたとき、
$$Q_1=C_1V+C_2V=(C_1+C_2)V$$
$$V=\frac{Q_1}{C_1+C_2}=\frac{0.3}{4.0×10^{-3}+2.0×10^{-3}}=50[V]$$
となる。
したがって、総静電エネルギーは、
$$W_2=\frac{1}{2}C_1V^2+\frac{1}{2}C_2V^2=7.5[J]$$
となる。
よって、抵抗で消費された電気エネルギーは
$$ΔW=W_1-W_2=11.25-7.5=3.75[J]$$
したがって、答えは(3)となる。
※以下参照

問11:電子理論
問題
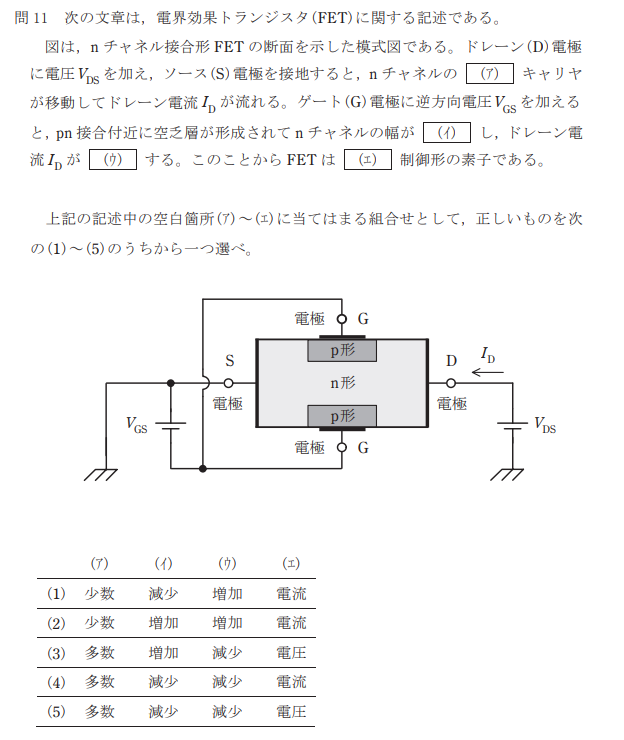
解説
文章の通り。
(5)が答えになる。

問12:電子理論
問題

解説
電子のエネルギー変化に伴う、速度の変化は次の式で求められる。
$$v’=v×\sqrt{\frac{W’}{W}}$$
よって、
$$v’= 1.19×10^7×\sqrt{\frac{100}{400}}=5.95×10^6[m/s]$$
したがって、答えは(2)となる。

問13:電子理論
問題
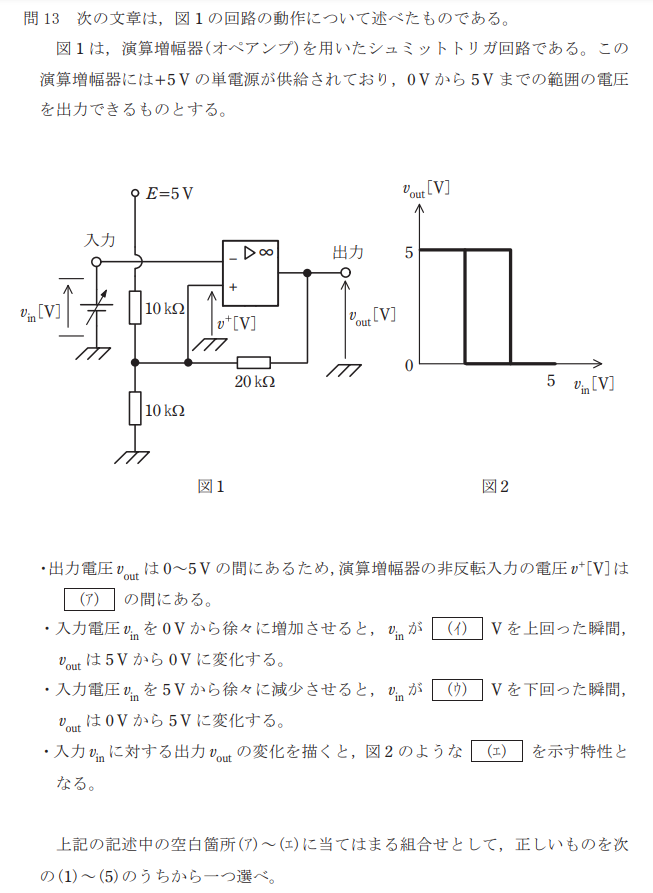
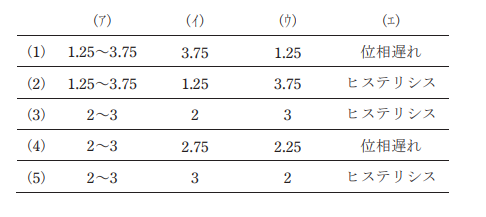
解説
文章の通り。
(5)が答えになる。

問14:電気測定
問題

解説
文章の通り。
(1)が答えになる。


