理論その７　電子理論(Electronic Theory)

半導体の特性

• 半導体は温度が上がると、電気抵抗率が低下する。(電気が流れやすくなる。)

半導体の種類

真性半導体

• 電子と正孔(正の電荷)が同数。ケイ素(Si)など。

不純物半導体

• 電子と正孔の数が異なる。どちらが多いかで以下のように性質が変化する。

n型半導体

• 価電子を3個持つ原子を真性半導体に加えたもの。ヒ素、リンなど。
  ⇒電子が1個余る。
  ※この場合、ヒ素やリンのことを「ドナー」という。

p型半導体

• 価電子を5個持つ原子を真性半導体に加えたもの。ほう素、インジウムなど。
  ⇒正孔が1個生まれる。
  ※この場合、ほう素やインジウムのことを「アクセプタ」という。

キャリア

• 電荷を運ぶ役割のこと(電子または正孔)

n型半導体

• 多数キャリア：電子
• 少数キャリア：正孔

ｐ型半導体

• 多数キャリア：正孔
• 少数キャリア：電子

ドリフト電流

• キャリアが、電界の力を受けて流れる電流。

拡散電流

• 電子や正孔は多いところから少ないところへ移動する。

ダイオード

• 電流を１方向(p型(アノード)→n型(カソード))にしか流さない半導体。

空乏層

• n型半導体とp型半導体の接合面付近で拡散したキャリアが互いに結合して消滅し(キャリアの再結合)、キャリアのない領域(空乏層)が生まれる。
  ⇒空乏層では電流は流れない。

※空乏層では、p型の接合面付近に負電荷が集まり、n型の接合面付近に正電荷が集まることで、n型からp型に向かって電界が生じる。

ダイオードの特性と種類

• ダイオードに順電圧(p型⇒n型)をかけると、空乏層で生じる電界と打ち消しあって、空乏層が消滅し急激に電流が流れ始める。(短絡状態)
• 反対に逆電圧(n型⇒p型)をかけると、空乏層が広がり、電流が流れにくくなる。(解放状態)
  しかし、さらに大きい逆電圧をかけると、急に大きな電流が流れ始める。(降伏現象)

定電圧ダイオード

• 降伏電圧付近では、電圧がほぼ一定になる性質を利用したダイオード。
• 一定の電圧を得る目的で使われる。

可変容量ダイオード

• 逆電圧をかけて、空乏層の接合容量(静電容量)を変化させる。
  ⇒接合容量Cは空乏層dの幅に反比例する。(\(C∝\frac{1}{d}\))

※コンデンサに似た役割を持つ。
　テレビやラジオなどの通信機器の同調回路などに用いられる。

発光ダイオード(LED)

• 順電流を流すと光るダイオード。

※キャリアの再結合が発生したときに光が生じる。
　ガリウム等を用いた半導体。
　消費電力が小さく長寿命。
　順方向の電圧降下は大きい(２V)

レーザーダイオード

• 順電流を流した時に発生する光を活性層に閉じ込め、一定以上に集めたときに放出される(誘導放出)。
• 同波長、同位相の光が発生する。

※光通信や光情報機器の光源として用いられる。

ホトダイオード

• 光を当てると、光の量に比例して電流が流れる(光起電力効果)
• p型に正電荷、n型に負電荷が集まる。

※太陽電池などに用いられる。

トランジスタについて

• 半導体の性質を利用して、電気の流れをコントロールする素子。

バイポーラトランジスタ

• ２種類のキャリアで働く。

以下、頻出されるエミッタ接地の場合を紹介する。

npn形トランジスタ

• n形(C,E)半導体でp形(B)半導体を挟む。

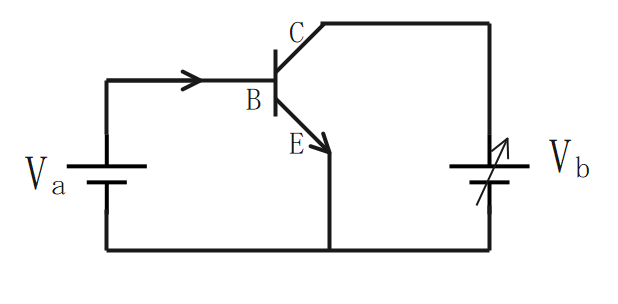
①順方向に電圧\(V_a\)を掛けることで、B-E間の空乏層が狭くなり、E→Bに電子が流れ込む。

②流れた電子は、一部は\(V_a\)に流れ、その他大部分はCを通って\(V_b\)に流れる。

【電子の流れ】E → B,C
【電流の流れ】B,C → E

エミッタ電流

 エミッタ電流は、ベース電流とコレクタ電流の和になる。

直流電流増幅率

特性

• 消費電力がFETより大きい。
• ベース電流によって、コレクタ電流を制御する電流制御素子
• 入力インピーダンスはFETより小さい。
• コレクタ電流は自由電子と正孔の両方が関与する。
• 静電気に対して、FETより破壊されにくい。

電界効果トランジスタ(FET)

• １種類のキャリアで働く。

接合形FET(npn形)

①逆電圧\(V_a\)を掛けることで、G-D,S間の空乏層が広がり、キャリアが通りにくくなる。

【電子】S → D
【電流】D → S

絶縁ゲート形FET(MOSFET)

• ゲート(G)に薄い絶縁膜を張り付けたFET

①順電圧\(V_g\)をかけると、G付近に電子が集まり、電子の通り道(チャネル)ができる。（エンハンスメント形）

②できたチャネルを、電流(電子)が流れる。

特性

• ゲート電圧\(V_g\)によって、ドレーン電流(Id)を制御する電圧制御素子。
• ゲート電圧\(V_g\)は、自由電子または正孔のどちらか一方に関与する。

電子放出

熱電子放出

• ある金属を熱すると、電子が表面から放出される。
  (例)タンタル(Ta)

二次電子放出

• 電子を金属またはその酸化物、ハロゲン化物などに衝突させると、その表面から新たな電子が放出される。

電界放出

• ある金属表面の電界強度を十分に大きくすると、常温でも電子が表面から放出される。
  (例)タングステン(W)

光電子放出

• 物質に光を当てると、光エネルギーによって物質内の電子が表面から外に放出される。

電子の運動

• 電界中に電子を置くと、電界とは逆向き(＋の方向)に力が働く。

電界中の電子のエネルギ―保存則

• 電界によって作用する力

位置エネルギー

運動エネルギー

エネルギー保存則

電子の速度

 電子の変化後の速度は、変化前の速度に変化前の静電エネルギーと変化後の静電エネルギーの比を掛けた値となる。

ローレンツ力

• 磁界中に、磁界の向きと直角に電子が突入した場合、電子の運動方向に対し直角方向に力(ローレンツ力)を受けて、等速円運動を行う(サイクロトン運動)。

※磁界の向きに対して角度を持って突入した場合は、らせん運動を行う。
　磁界の向きに対して平行に突入した場合は、ローレンツ力は働かず等速直線運動を行う。

• フレミングの左手の法則を使うと、ローレンツ力の向きが分かる。
  ・中指と反対の方向：電子の運動の向き
  ・人差し指：磁界の向き
  ・親指：ローレンツ力の向き

サイクロトン運動(等速円運動)

• ローレンツ力(向心力)と遠心力が釣り合うことで、電子は等速円運動を描く。

静電力

• 電界中に電子を置くと、電子は電界の向きと反対方向に静電力を受ける。
• 電子が電界の向きに対して角度を持って突入した場合は、その軌跡は放物線を描く。

増幅度

• 入力信号と出力信号の比

電圧増幅度

電流増幅度

電力増幅度

演算増幅器(OPアンプ)

• ２つの入力端子から、1つの出力を行う増幅器。

理想的な演算増幅器

• どんな周波数の電圧でも増幅ができる。
• 入力端子・出力端子は、入力・出力するとき電圧降下しない。
  →入力インピーダンス∞、出力インピーダンス０にする。
• 小さな入力信号を無限大まで増幅させて出力できる。

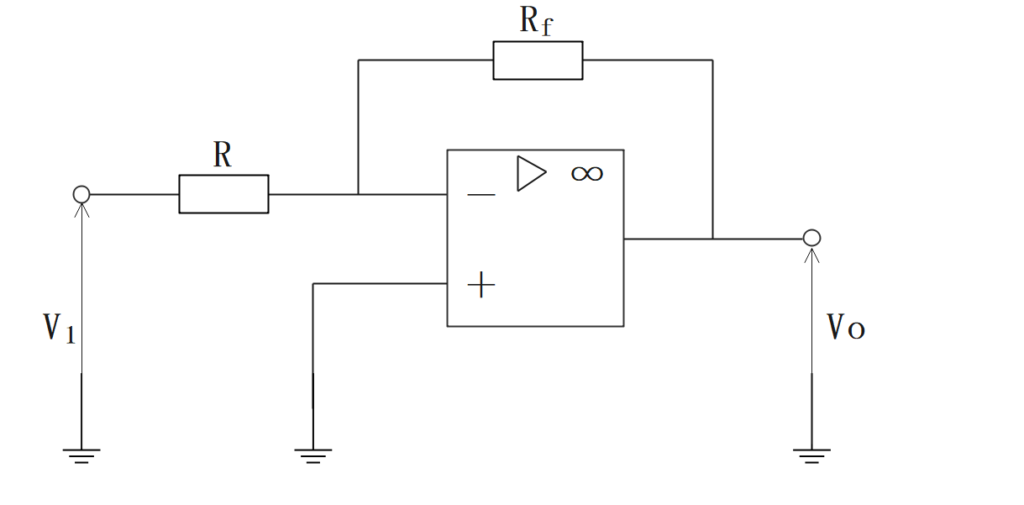
反転増幅回路

• 入力電圧と出力電圧の符号が逆になる。

非反転増幅回路

• 入力電圧と出力電圧の符号が同じになる。

発振回路

発信回路の振幅条件

• 増幅回路の入力電圧と帰還回路の出力電圧を同相にする。
• 増幅回路の入力電圧≦帰還回路の出力電圧とする。

あわせて読みたい

理論その８　電気測定(Electrical Measurements) このページについて このページでは、電気測定の公式や重要単語とその解説について掲載しています。また、その公式がどの過去問に使われているかについても記載していま...