理論その3 電磁気(Electromagnetic)

このページでは、電磁気の公式や重要単語とその解説について掲載しています。
また、その公式がどの過去問に使われているかについても記載しています。
電磁気の分野では、各形状導体に電流を流した時の磁界の大きさや電磁力の大きさ、誘導起電力を求める計算問題などが出題されます。
また、レンツの法則など知識を問われる問題も出題されます。覚えていると簡単に解くことのできる問題が多いので、しっかり勉強しましょう。
磁力の大きさ
磁極間に働く力は、磁荷(磁極の強さ)の積に比例し、磁極間の距離の2乗に反比例する。
$$\Large{F = k_m\frac {m_1m_2}{r^2}}$$
\(F\):磁力の大きさ[N] \(k_m\):比例定数 \(m\):磁荷(磁極の強さ)[Wb] \(r\):距離[m]
*真空中:\(k_m=6.33×10^4\)
磁界で働く磁力の大きさ
磁力の大きさは、磁荷と磁界の大きさの積に比例する。
$$\Large{F = mH}$$
\(F\):磁力の大きさ[N] \(m\):磁荷[Wb] \(H\):磁界の大きさ[A/m]
磁力線の性質
- N極からS極に流れる架空の線。
- 磁力線は互いに交わったり、折れ曲がったり、消えたり、枝分かれしない。
- 磁力線の接線の向きが、磁界の向きとなる。
- 磁力線は磁石の中を通らない(磁束は通る)
ガウスの法則(磁力線)
周囲の媒質が誘電率μである磁荷+m(-m)からは、次の式の本数だけ磁力線が出る(入る)。
$$\Large{N = \frac {m}{μ}}$$
\(N\):電気力線 \(m\):磁荷[Wb] \(μ\):透磁率[H/m]
磁界の大きさ
磁界の大きさは、単位面積当たりの磁力線の本数となる。
$$\Large{H = \frac {N}{A}=\frac {m}{4πμr^2}}$$
\(H\):磁界の大きさ[A/m] \(N\):磁力線の本数 \(A\):球の表面積[m2] \(m\):磁荷[Wb] \(μ\):透磁率[H/m] \(r\):距離[m]
磁束密度
磁束密度は、磁束に比例し、球の表面積に反比例する。
$$\Large{B = \frac {Φ}{A}}$$
\(B\):磁束密度[T] \(Φ\):磁束[Wb] \(A\):球の表面積[m2]
*磁束:周りの空気の影響を考慮しない(真空中)
磁束密度と磁界の大きさ
磁束密度は、透磁率と磁界の大きさの積に比例する。
$$\Large{B = μH=μ_0μ_rH}$$
\(B\):磁束密度[T] \(μ\):透磁率[H/m] \(μ_0\):真空中の透磁率[H/m] \(μ_r\):比透磁率 \(H\):磁界の大きさ[A/m]
電流と磁界の向き(右ねじの法則)
導体に電流を流した時にできる磁界の向きを表したものを磁力線という。
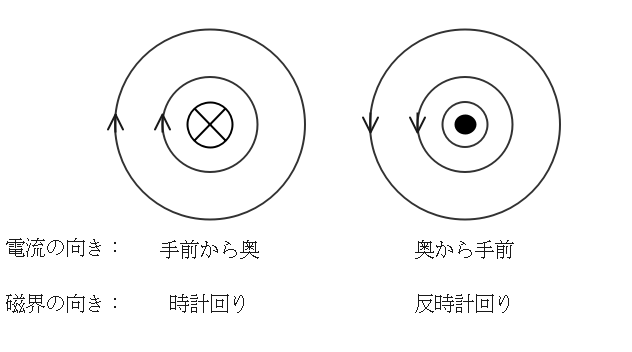
レンツの法則
磁界の向きはN極の向いている方向となる。
磁束の変化を妨げる方向に誘導起電力が発生する。
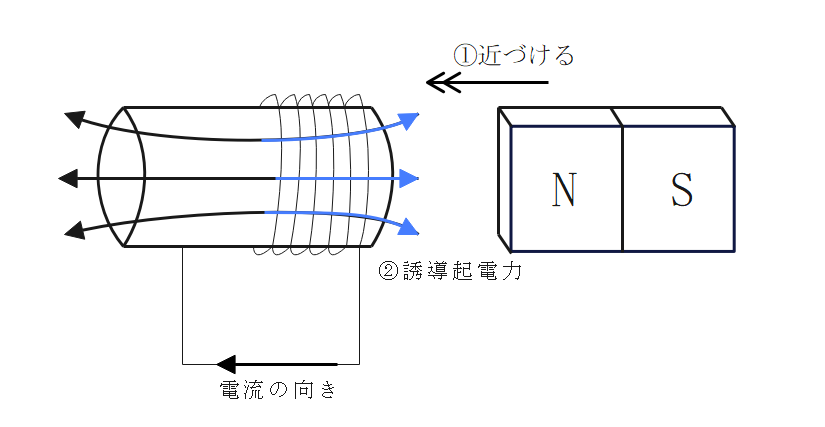
電流と磁界の大きさ
直線状導体
直線状導体に電流を流した時にその周りに発生する磁界の大きさは、電流の大きさに比例し、導体と磁界の距離に反比例する。
$$\Large{H = \frac {I}{2πr}}$$
\(H\):磁界の大きさ[A/m] \(I\):電流[A] \(r\):距離[m]
円形コイル
円形コイルに電流を流した時その周りに発生する磁界の大きさは、コイルの巻数と電流の大きさの積に比例し、導体と磁界の距離に反比例する。
$$\Large{H = \frac {NI}{2r}}$$
\(H\):磁界の大きさ[A/m] \(N\):巻数 \(I\):電流[A] \(r\):距離[m]
無限長ソレノイド
無限長ソレノイドに電流を流した時その周りに発生する磁界の大きさは、コイルの巻数と電流の大きさの積に比例する。
$$\Large{H = NI}$$
\(H\):磁界の大きさ[A/m] \(N\):巻数 \(I\):電流[A]
環状ソレノイド
環状ソレノイドに電流を流した時その周りに発生する磁界の大きさは、コイルの巻数と電流の大きさの積に比例し、導体と磁界の距離に反比例する。
$$\Large{H = \frac {NI}{l} = \frac {NI}{2πr}}$$
\(H\):磁界の大きさ[A/m] \(N\):巻数 \(I\):電流[A] \(l\):磁路の長さ[m] \(r\):距離[m]
電磁力の大きさ
電磁力の大きさは、磁束密度と電流の大きさに比例する。
$$\Large{F = BlIsinθ}$$
\(F\):電磁力の大きさ[N] \(B\):磁束密度[T] \(l\):導体の長さ[m] \(I\):電流[A] \(θ\):磁界と導体のなす角
平行導体間に働く電磁力の大きさ
電磁力の大きさは、透磁率と2本の導体に流れる電流の大きさの積に比例し、2本の導体間距離に反比例する。
$$\Large{f = \frac {μI_aI_b}{2πr}}$$
\(f\):単位長さ当たりの電磁力の大きさ[N/m] \(μ\):透磁率[H/m] \(I\):電流[A] \(r\):導体間距離[m]
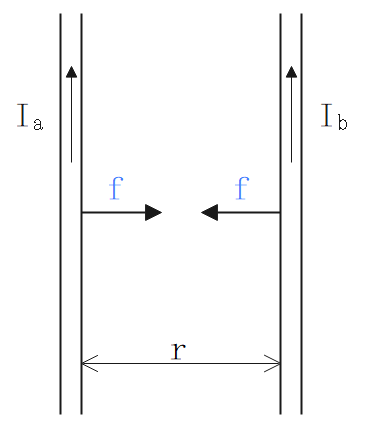
反発力(斥力)
2本の平行導体に逆向きの電流を流した時、右ねじの法則より内側の磁界を強め合って、平行導体間に反発力(斥力)が働く。
吸引力
2本の平行導体に同じ向きの電流を流した時、右ねじの法則より内側の磁界を打ち消しあって平行導体間に吸引力が働く。
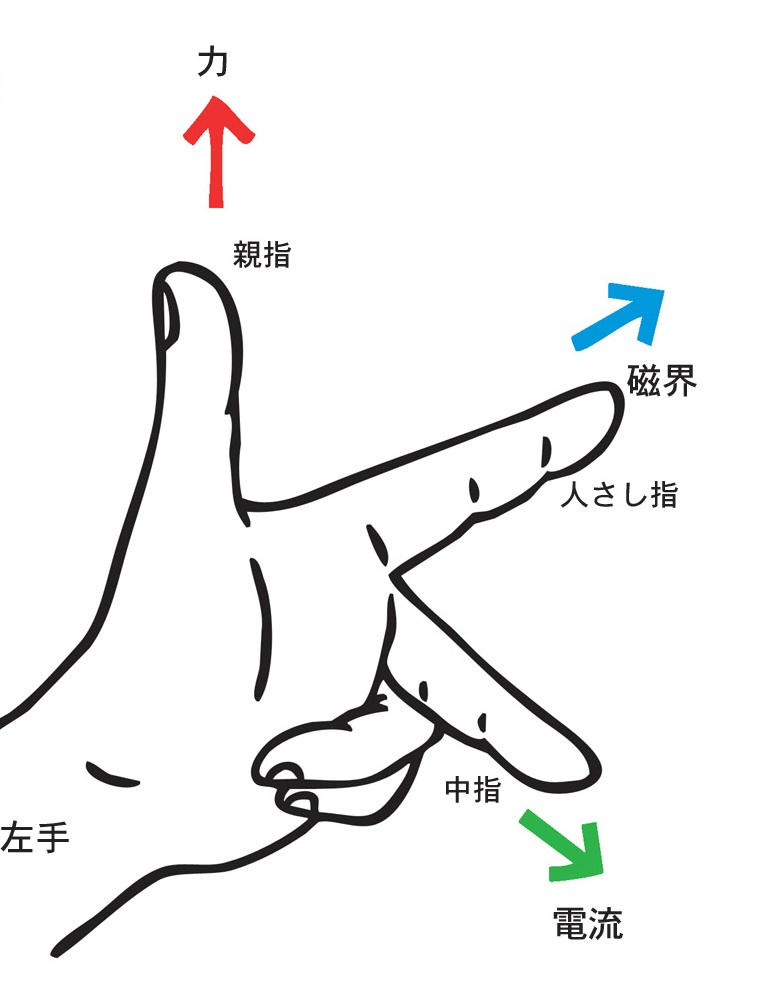
フレミングの左手の法則
- 電動機の原理を示す。
- 3本の指でx,y,z軸を作るように形を作り、2つの向きに合わせると、もう1つの向きが求められる。
- 中指:電流の向き、人差し指:磁界の向き、親指:電磁力の向き
コイルに働くトルク
トルクの大きさは、磁束密度と電流の大きさの積に比例する。
$$\Large{T = FDcosθ = BlIDcosθ}$$
\(T\):トルク[N/m] \(F\):電磁力の大きさ[N] \(D\):腕の長さ[m] \(θ\):力を加える角[°] \(B\):磁束密度[T]\(l\):導体の長さ[m] \(I\):電流[A]
起磁力
起磁力は、コイルに流れる電流とコイルの巻数の積に比例する。
$$\Large{F_m = NI}$$
\(F_m\):起磁力[A] \(N\):巻数 \(I\):電流[A]
磁気回路におけるオームの法則
形は電気回路のオームの法則と同じ。
磁気回路は、電気回路の各パラメータと以下のように対応させる。
- 磁気抵抗\(R_m\) ⇔ 電気抵抗\(R\)
- 起磁力\(NI\) ⇔ 電源電圧\(E\)
- 磁束\(Φ\) ⇔ 電流\(I\)
- 透磁率\(μ\) ⇔ 導電率\(σ\)
$$\Large{R_m = \frac {NI}{Φ}}$$
\(R_m\):磁気抵抗[H-1] \(N\):巻数 \(I\):電流[A]
鉄心の抵抗(磁気抵抗)
断面積\(Am^2\)、長さl[m]の鉄心が持つ磁気抵抗。
$$\Large{Rm = \frac {l}{μA}}$$
\(R_m\):磁気抵抗[H-1] \(l\):磁路の長さ[m] \(μ\):透磁率[H/m] \(A\):断面積[m2]
磁気抵抗の直列接続
計算方法は電気回路の合成抵抗と同じ。
$$\Large{R_{mo} = R_{m1}+R_{m2}+\cdots+R_{mn}}$$
\(R_m\):磁気抵抗[H-1]
磁気抵抗の並列接続
計算方法は電気回路の合成抵抗と同じ。
$$\Large{R_{mo} = \frac {1}{\frac {1}{R_{m1}}+\frac {1}{R_{m2}}+\cdots+\frac {1}{R_{mn}}}}$$
\(R_m\):磁気抵抗[H-1]
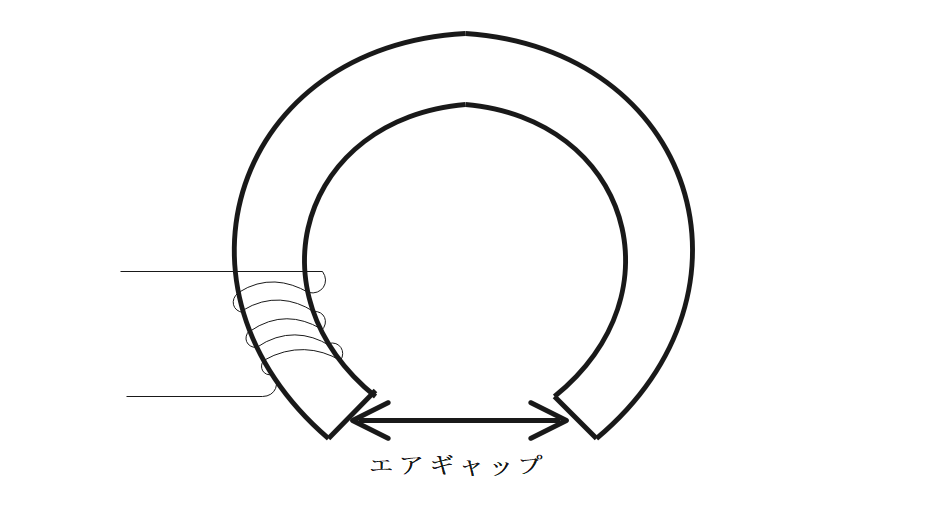
エアギャップ
鉄心に存在するすきま。1つの磁気抵抗\(R_m\)として考える。
磁気飽和
磁化力(磁界の大きさ)を大きくすると、磁束密度はB=μHより増加するが、さらに磁化力を大きくすると、あるところで増加しなくなる現象。
ファラデーの電磁誘導の法則
誘導起電力は、コイルの巻数と磁束[Wb]の変化量の積に比例し、時間の変化量に反比例する。
$$\Large{e = -N\frac {△Φ}{△t}}$$
\(e\):誘導起電力[V] \(N\):巻数 \(Φ\):磁束[Wb] \(t\):時間[s]
磁束鎖交数
$$\Large{ψ = NΦ}$$
\(ψ\):磁束鎖交数 \(N\):巻数 \(Φ\):磁束[Wb]
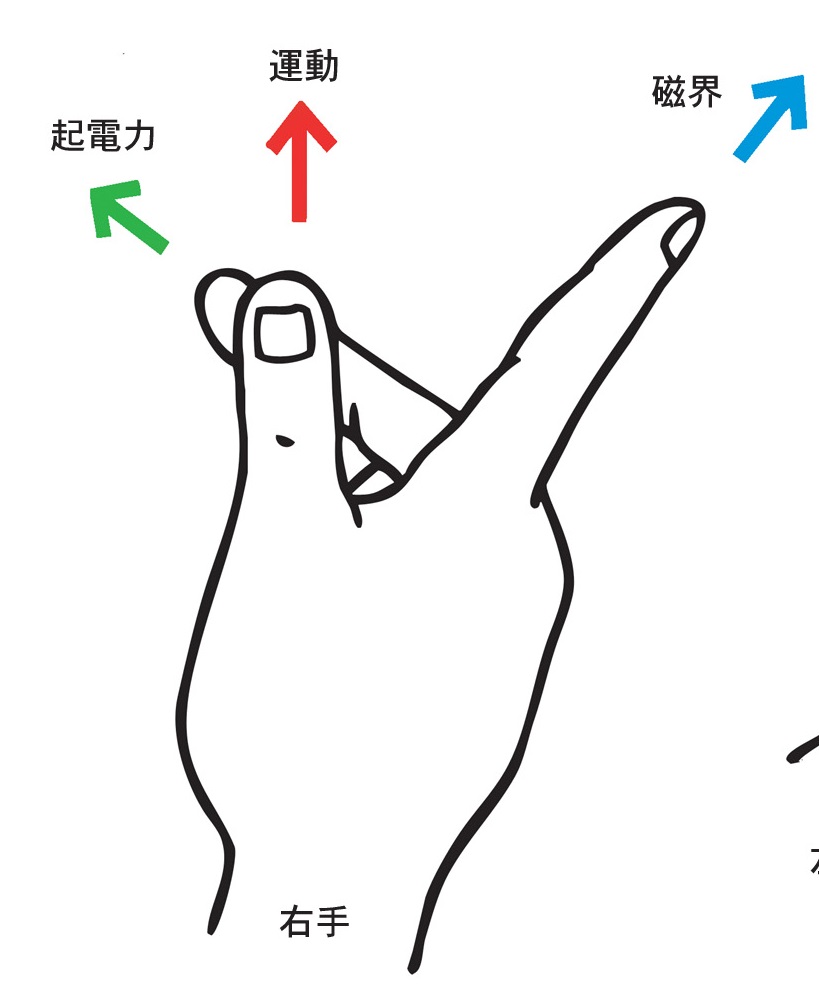
フレミングの右手の法則
- 発電機の原理を示す。
- 3本の指でx,y,z軸を作るように形を作り、2つの向きに合わせると、もう1つの向きが求められる。
- 中指:起電力の向き、人差し指:磁界の向き、親指:運動の向き
誘導起電力
誘導起電力は磁束密度、導体の長さ、導体の移動する速度、磁束密度の方向と導体が移動する方向のなす角の積に比例する。
$$\Large{e = Blvsinθ}$$
\(e\):誘導起電力[V] \(B\):磁束密度[T] \(l\):導体の長さ[m] \(v\):導体の移動する速度[m/s] \(θ\):磁束密度の方向と導体が移動する方向のなす角[deg]
自己誘導起電力
自己誘導起電力は、自己インダクタンスと電流の変化量の積に比例し、時間の変化量に反比例する。
$$\Large{e = -L\frac {△I}{△t}}$$
\(e\):自己誘導起電力[V] \(L\):インダクタンス[H] \(I\):電流[A] \(t\):時間[s]
自己インダクタンス
自己インダクタンスは、巻数と磁束の積(磁束鎖交数)に比例し、電流に反比例する。
$$\Large{L = \frac {NΦ}{I}}$$
\(L\):自己インダクタンス[H] \(N\):巻数 \(Φ\):磁束[Wb] \(I\):電流[A]
相互誘導起電力
相互誘導起電力は、相互インダクタンスとコイル1に流れる電流の変化量の積に比例し、時間の変化量に反比例する。
$$\Large{e_2 = -M\frac {△I_1}{△t}}$$
\(e_2\):コイル2の相互誘導起電力[V] \(M\):相互インダクタンス[H] \(I_1\):コイル1の電流[A] \(t\):時間[s]
相互インダクタンス
相互インダクタンスは、コイル2の巻数とコイル1とコイル2の両方を貫く磁束の積に比例し、コイル1に流れる電流に反比例する。
$$\Large{M = \frac {N_2Φ_{12}}{I_1}}$$
\(M\):相互インダクタンス[H] \(N_2\):コイル2の巻数 \(Φ_{12}\):コイル1とコイル2を貫く磁束[Wb]
\(I_1\):コイル1の電流[A]
$$\Large{M = k\sqrt{L_1L_2}}$$
\(M\):相互インダクタンス[H] \(k\):結合係数 \(L\):自己インダクタンス[H]
$$\Large{k = \frac {M}{\sqrt{L_1L_2}}}$$
\(k\):結合係数 \(M\):相互インダクタンス[H] \(L\):自己インダクタンス[H]
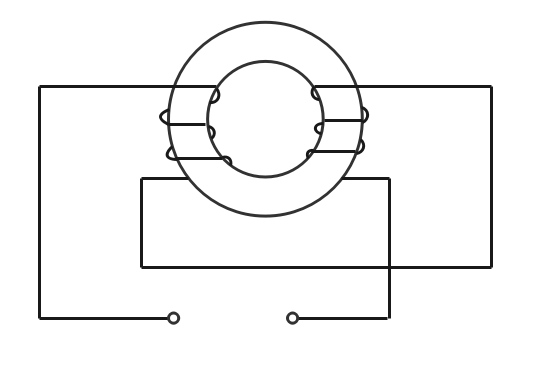
和動接続の合成自己インダクタンス
一次コイルと二次コイルが作る磁界が同じ向きになる接続方法
$$\Large{L = L_1+L_2+2M}$$
\(L\):自己インダクタンス[H] \(M\):相互インダクタンス[H]
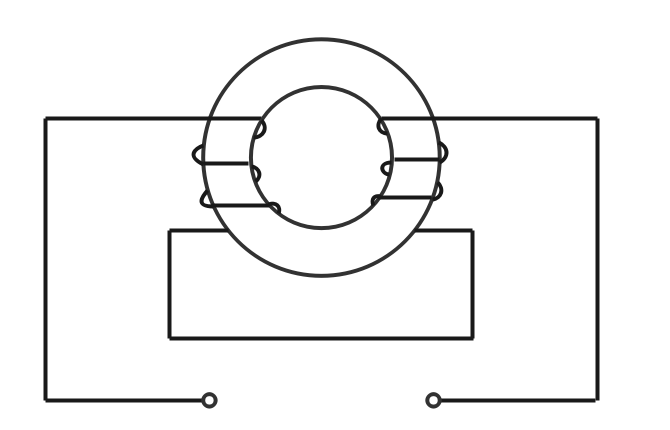
差動接続の合成自己インダクタンス
一次コイルと二次コイルがつくる磁界が反対になる接続方法
$$\Large{L = L_1+L_2-2M}$$
\(L\):自己インダクタンス[H] \(M\):相互インダクタンス[H]
電磁エネルギー
電磁エネルギーは、自己インダクタンスと電流の2乗の積に比例する。
$$\Large{W = \frac {1}{2}LI^2}$$
\(W\):電磁エネルギー[J] \(L\):自己インダクタンス[H] \(I\):電流[A]


