理論その1 直流回路(Direct Current)

このページでは、直流回路の公式や重要単語とその解説について掲載しています。
また、その公式がどの過去問に使われているかについても記載しています。
直流回路は理論に限らず、他科目でも適用される重要な単元です。
例年、2~3問問題として出題されています。
計算に関する公式が多いため、覚えると同時に問題を解いて、応用できるようにしましょう。
電流の基本
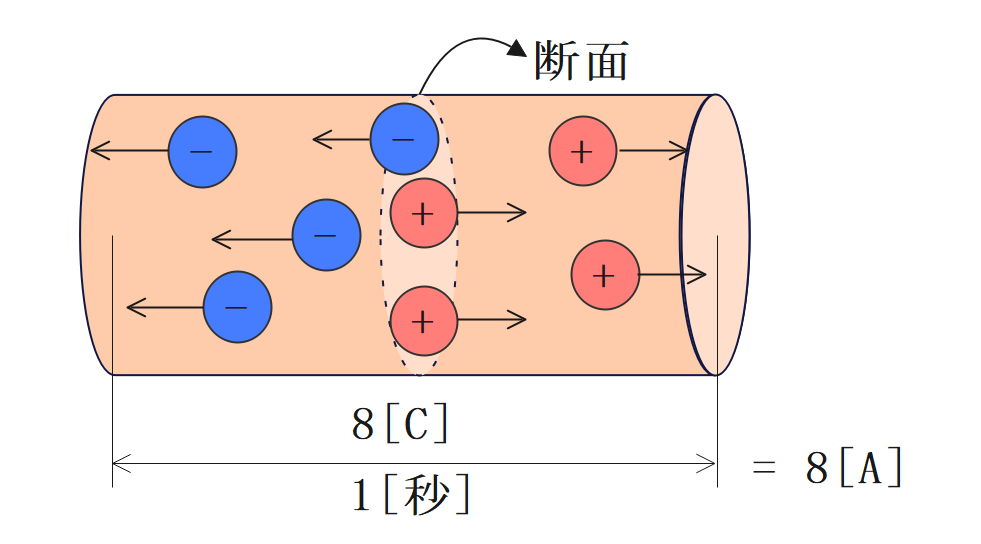
電流の大きさは、電荷量に比例し時間に反比例する。
$$\Large{I = \frac {Q}{t}}$$
\(I\)[A]:電流 \(Q\)[C]:電荷 \(t\)[s]:時間
オームの法則
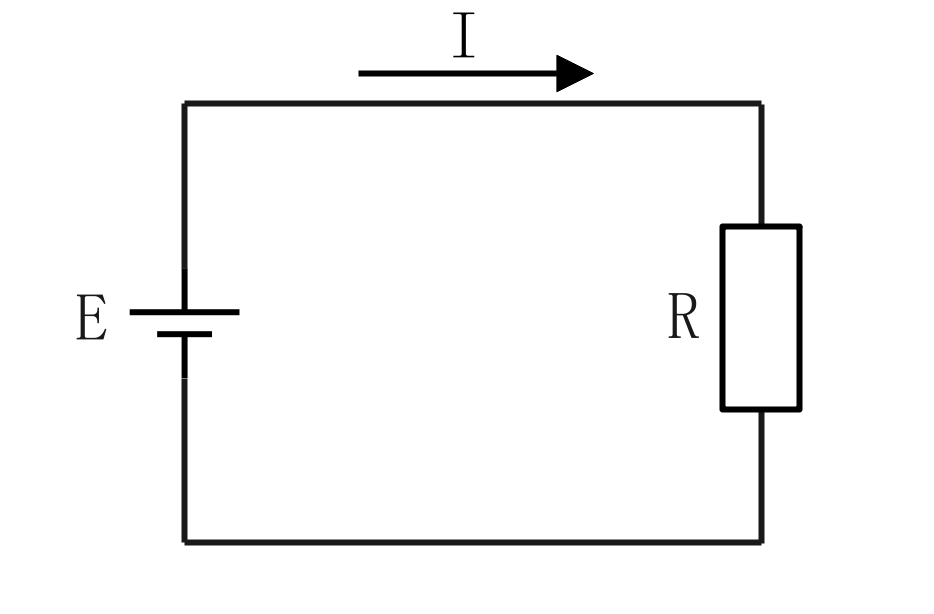
電流は、電圧に比例し、抵抗に反比例する。
$$\Large{I = \frac{E}{R}}$$
\(I\)[A]:電流 \(E\)[V]:電位差 \(R\)[Ω]:抵抗
直列回路
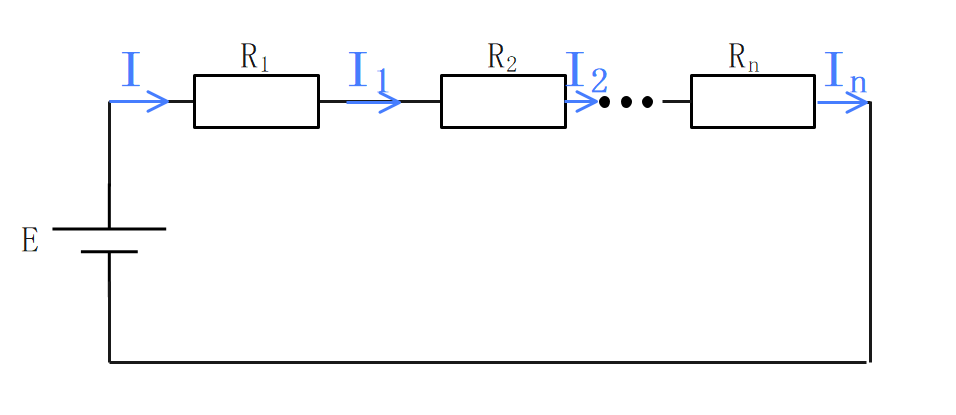
各抵抗に流れる電流は等しい。これを電流の連続性という。
$$\Large{I=I_1 = I_2 = \cdots = I_n}$$
合成抵抗
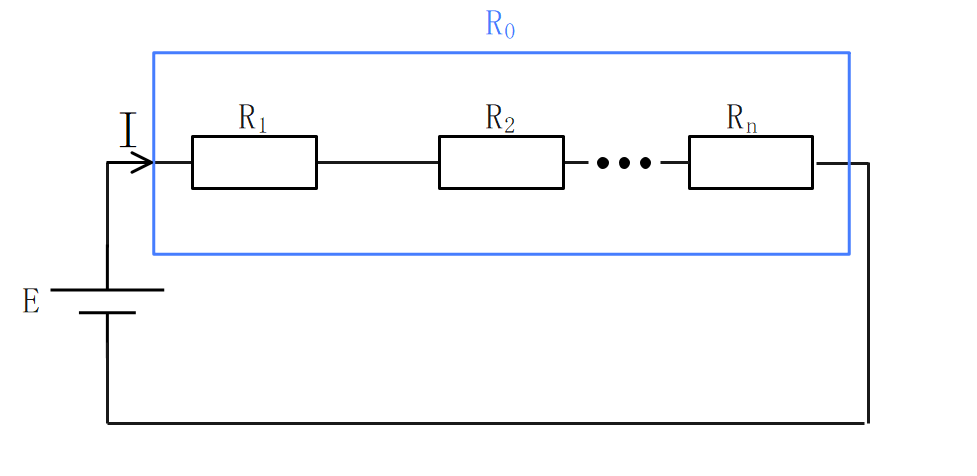
直列回路の合成抵抗は、各抵抗の和になる。
$$\Large{Ro=R_1 + R_2 + \cdots + R_n}$$
\(R_o\)[Ω]:合成抵抗
分圧
直列回路の全電圧は、各抵抗の抵抗値で比例分配される。
$$V_1 = E×\frac {R_1}{R_1+R_2+ \cdots + R_n}$$
\(R_o\)[Ω]:合成抵抗
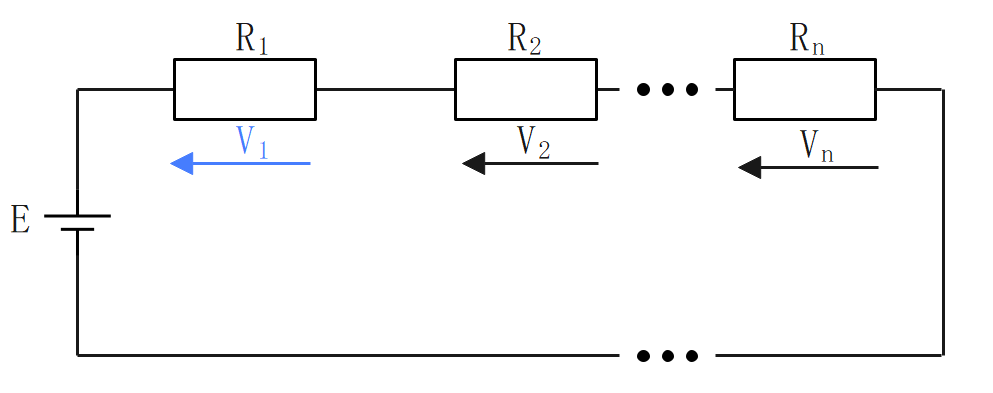
並列回路
各抵抗による電圧降下は等しい。
$$\Large{V_1=V_2 = \cdots = V_n}$$
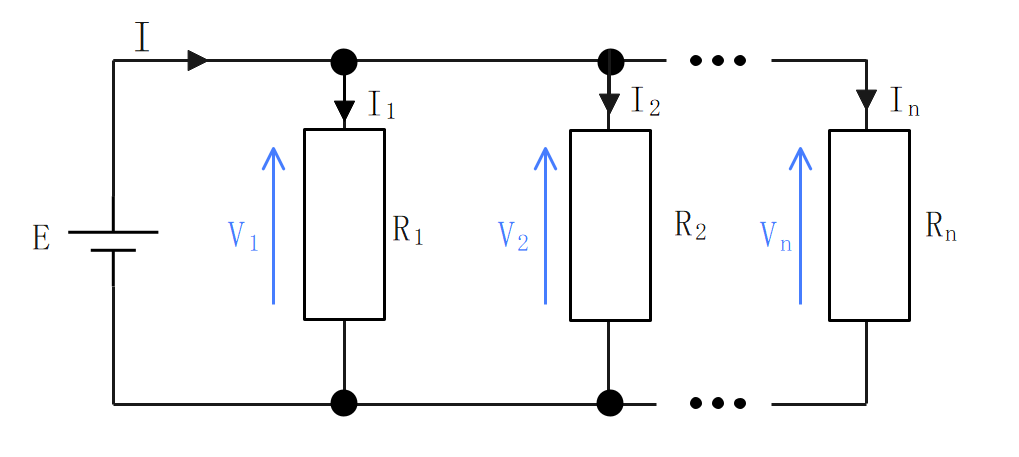
合成抵抗
並列回路の合成抵抗は、各抵抗の逆数の和の逆数になる。
$$\Large{R_o = \frac {1}{\frac {1}{R_1}+\frac {1}{R_2}+\cdots+\frac {1}{R_n}}}$$
\(R_o\)[Ω]:合成抵抗
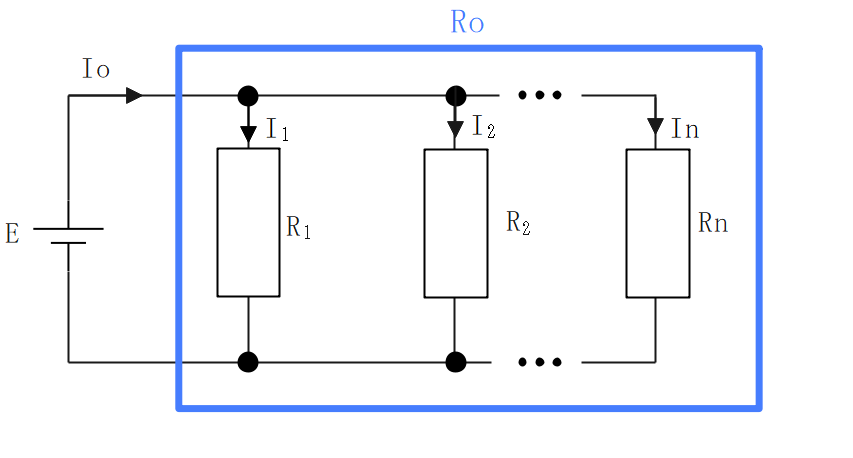
抵抗が2つのときは、次の式が使える。
$$\Large{R_o = \frac {R_1R_2}{R_1+R_2}}$$
\(R_o\)[Ω]:合成抵抗
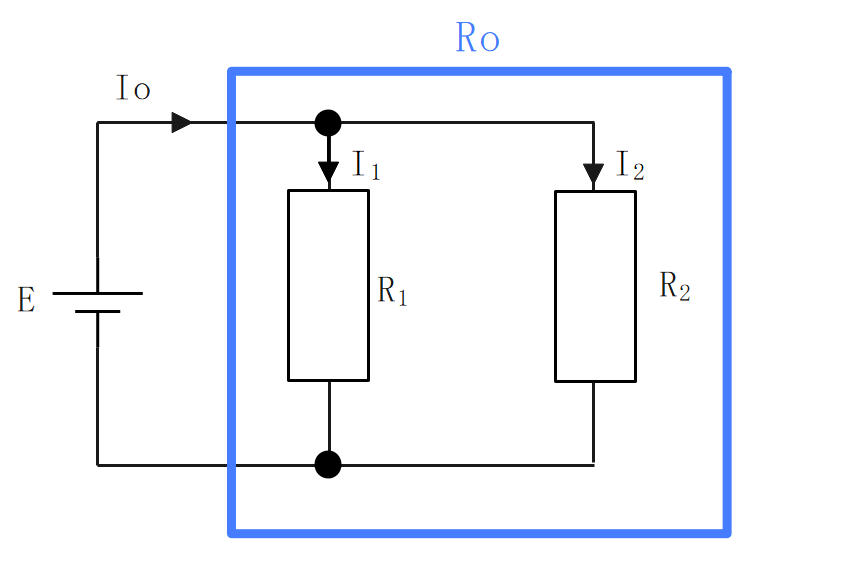
分流
並列回路の全電流は、各抵抗の抵抗値で逆比例分配(\(\frac{1}{R}\))される。
$$I_1 = I_0×\frac {\frac{1}{R_1}}{\frac {1}{R_1}+\frac {1}{R_2}+\cdots+\frac {1}{R_n}}$$
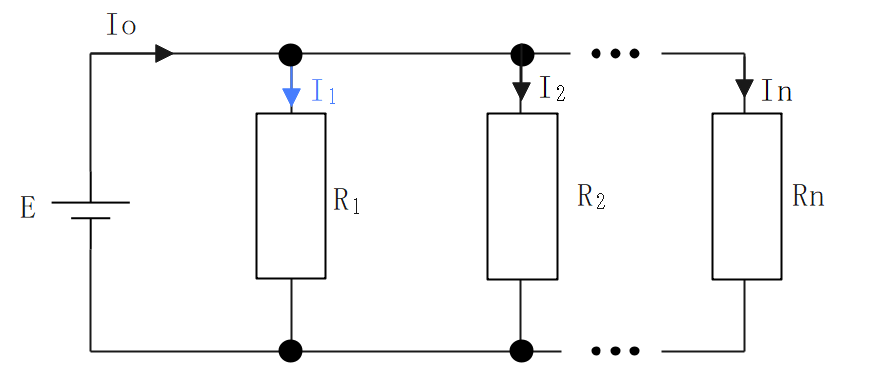
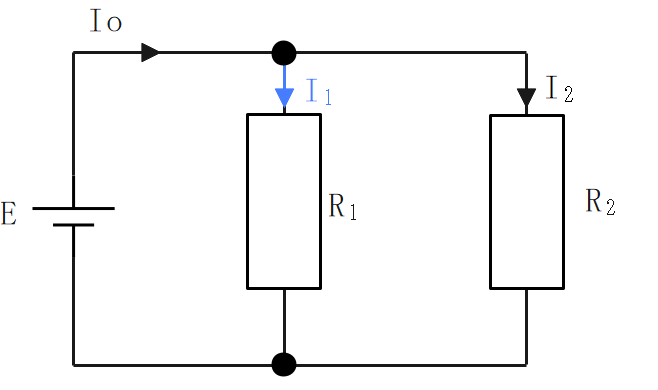
抵抗が2つのときは、次の式が使える。
$$\Large{I_1 = I_0×\frac {R_2}{R_1+R_2}}$$
キルヒホッフの法則
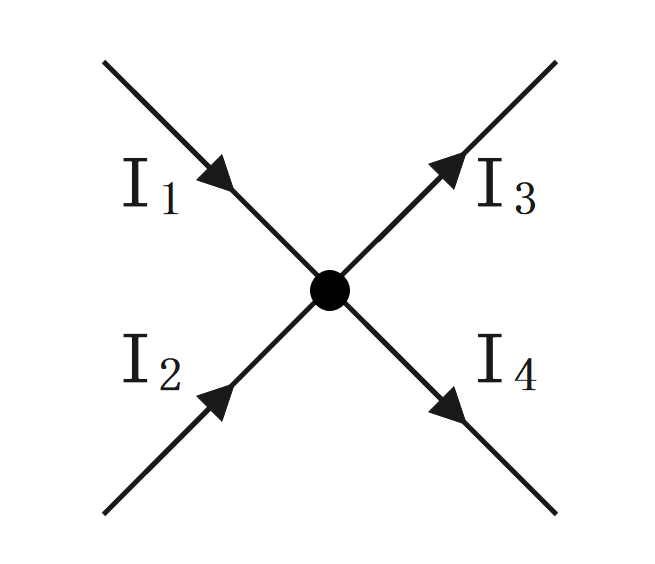
キルヒホッフの第一法則(電流則)
回路網の任意の接続点に流入・流出する電流の総和は 0である。
$$\Large{I_1+I_2 = I_3+I_4}$$
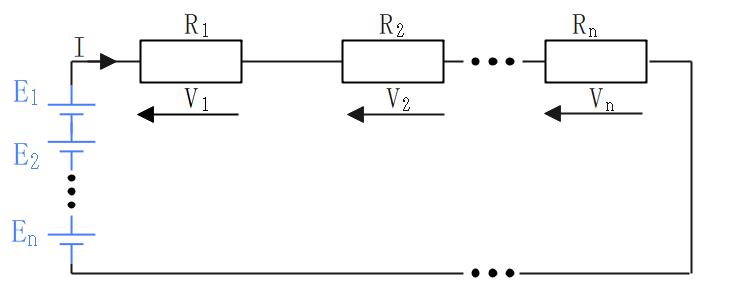
キルヒホッフの第二法則(電圧則)
回路網中の任意の閉路を一巡するとき、起電力の総和と電圧降下の総和は等しい。
$$\large{E_1+E_2+\cdots+E_n =\\ R_1I+R_2I+\cdots+R_nI}$$
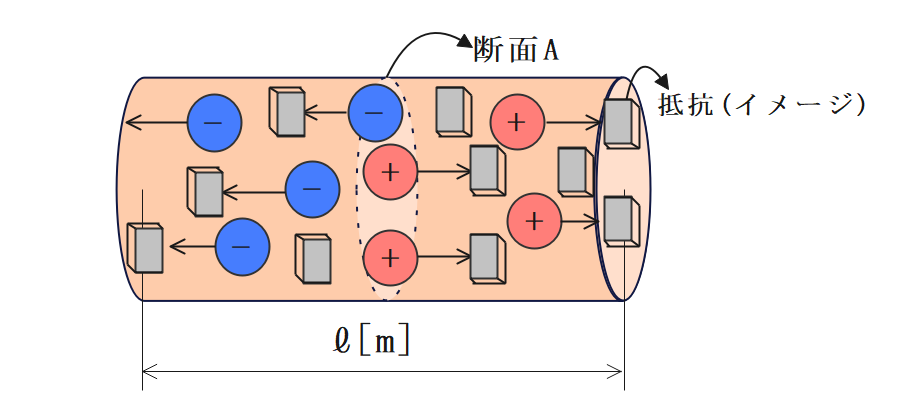
導体の抵抗
断面積\(Am^2\)、長さl[m]の導体が持つ抵抗値。
$$\Large{R = \frac {l}{σA}}$$
\(σ\)[S/m]:導電率 \(A\)[m2]:断面積 \(l\)[m]:長さ
\(σ=\frac{1}{ρ}\)
\(ρ\)[Ω・m]:抵抗率
温度変化による抵抗値
導体の温度が上昇すると、抵抗値は大きくなる。
$$\Large{R_2 =R_1(1+α_1(t_2-t_1))}$$
\(R_1\)[Ω]:温度変化前の抵抗値 \(R_2\)[Ω]:温度変化後の抵抗値
\(t_1\)[℃]:変化前の温度 \(t_2\)[℃]:変化後の温度 \(α_1\):温度変化前の抵抗温度係数
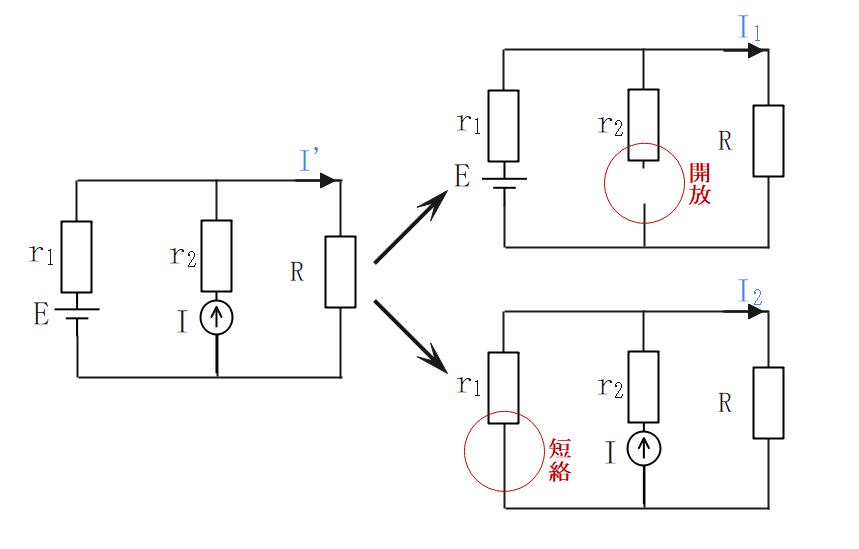
重ね合わせの理
複数の電源がある回路で、回路の任意の点の電流は、各電源が単独で存在した場合の値の和に等しい。
$$\Large{I’=I_1+I_2}$$
コンダクタンス
コンダクタンスは、抵抗の逆数つまり電流の流れやすさを表す。
$$\Large{G = \frac {1}{R}}$$
\(G\)[S]:コンダクタンス
テブナンの定理
回路網中にある抵抗に流れる電流を求める時、次の式を使う。
$$\Large{I = \frac {E_o}{R_o+R}}$$
\(E_0\)の求め方を以下に示す。
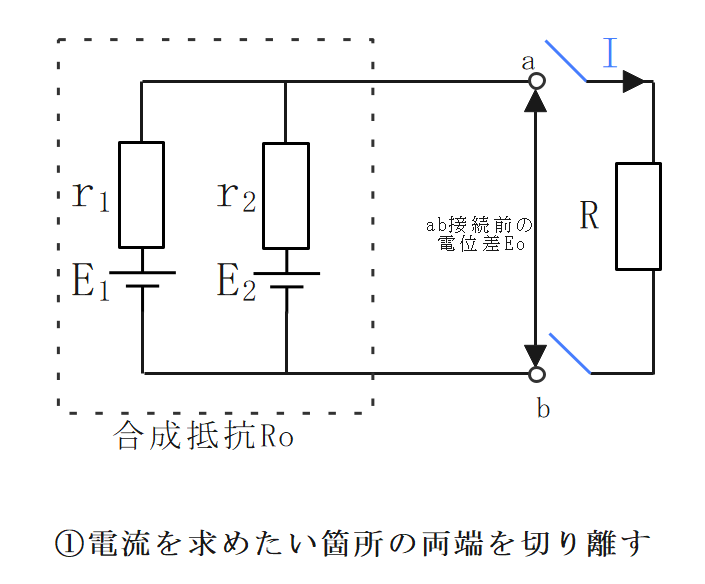
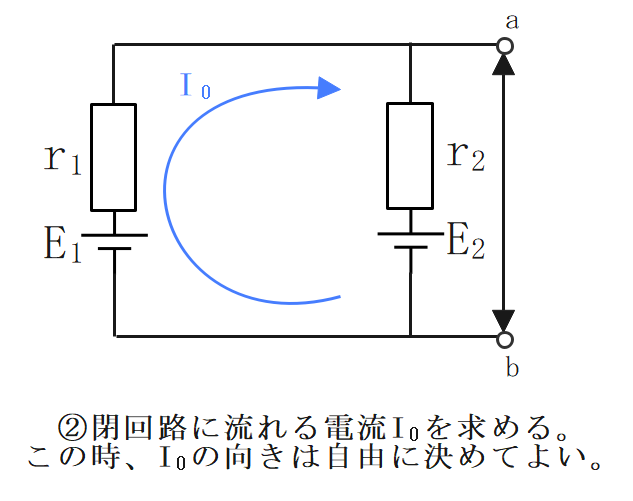
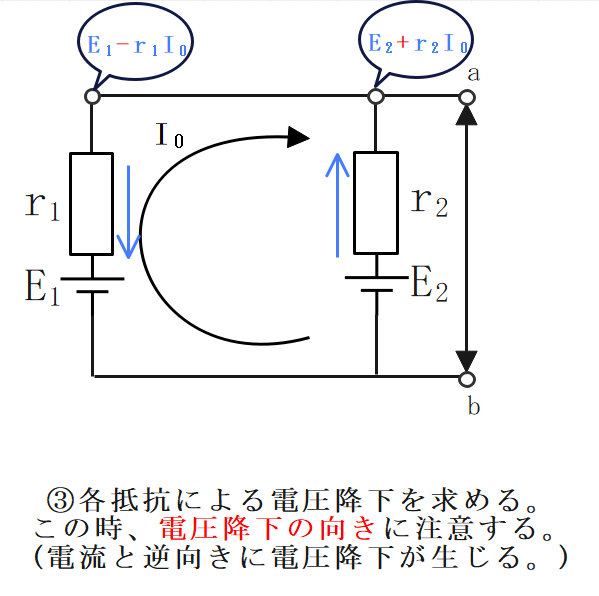
(例)\(E_1=20[V]、E_2=15[V]、r_1=2[Ω]、r_2=3[Ω]\)の時のa-b間の電位差\(E_0\)を求める。
①図①のように回路を切り離す。
②電流\(I_0\)の向きを図②の向きとする。
また電流\(I_0\)の値はオームの法則より、
$$I_0=\frac{E_1-E_2}{r_1+r_2}=\frac{20-15}{2+3}=1[A]$$
③どちらか一方の電圧を求める。\(E_1、r_1\)側で求めると、電圧Eは、
$$E=E_1-r_1I_0=20-2×1=18[V]$$
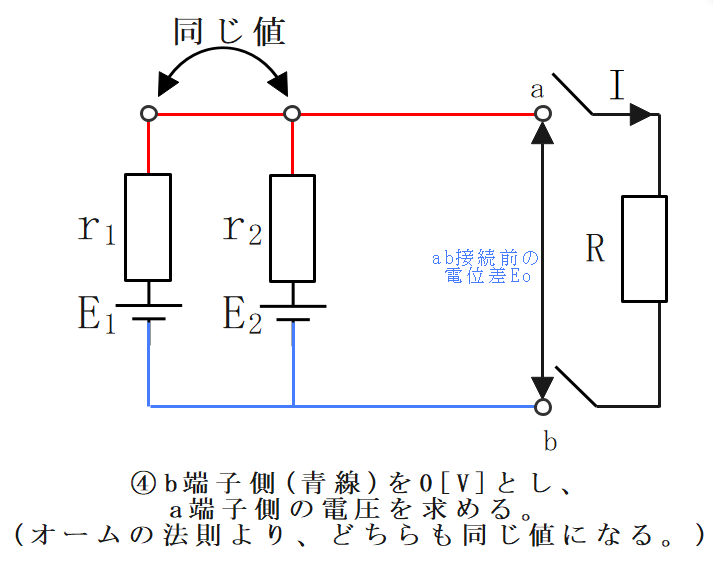
よってa-b間の電位差\(E_0\)は、
$$E_0=14-0=18[V]$$
ミルマンの定理
電源と抵抗が並列になっている回路の全電圧を求める時、次の式を使う。
$$V_{ab} =\frac{I}{G}=\frac {-\frac{E_1}{R_1}+\frac{E_2}{R_2}+\frac{E_3}{R_3}+\frac{0}{R_4}}{\frac {1}{R_1}+\frac {1}{R_2}+\frac {1}{R_3}+\frac {1}{R_4}}$$
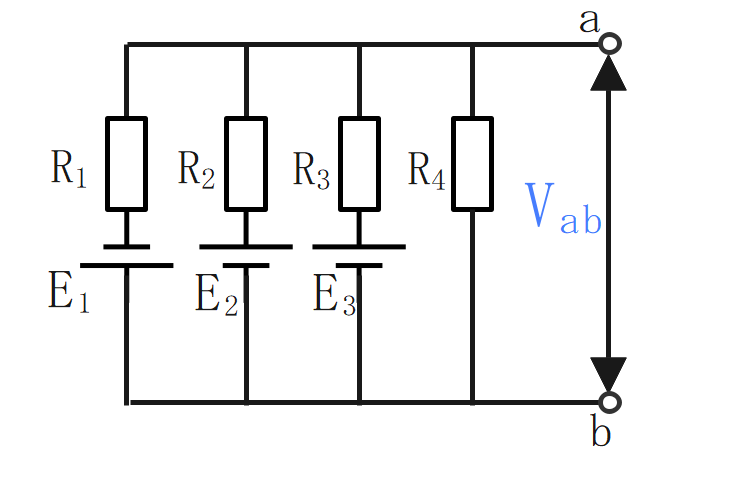
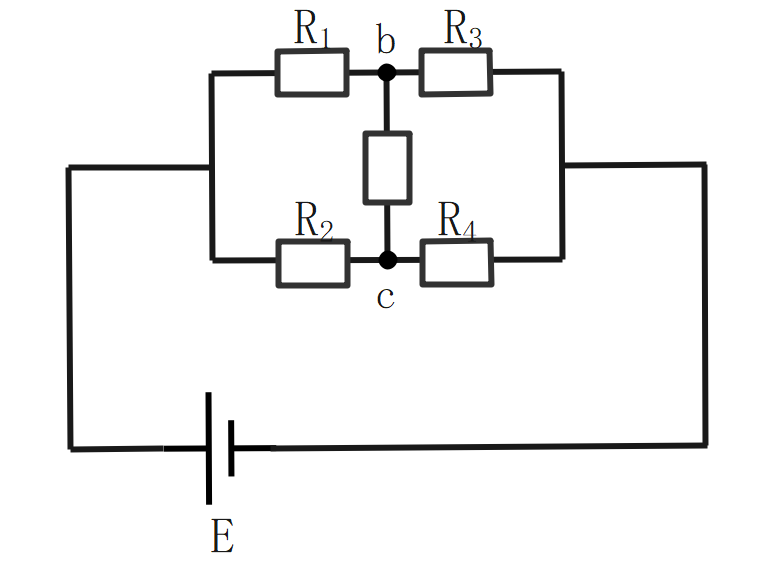
ホイートストンブリッジの平衡条件
\(R_1R_4=R_2R_3\)の時、bc間に電流は流れない。
Δ-Y変換(とY-Δ変換)
Δ接続とY接続は、相互に等価変換できる。
Δ-Y変換
\(\Large{R_1 = \frac {r_1r_2}{r_1+r_2+r_3}}\)
\(\Large{R_2 = \frac {r_2r_3}{r_1+r_2+r_3}}\)
\(\Large{R_3 = \frac {r_3r_1}{r_1+r_2+r_3}}\)
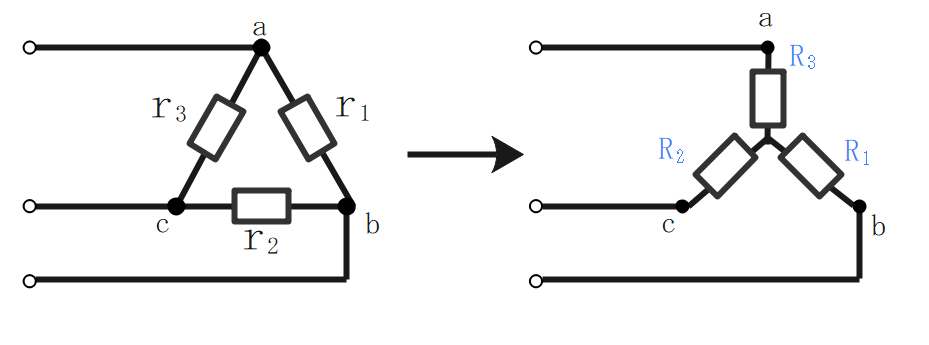
Y-Δ変換
\(r_1 = \frac {R_1R_2+R_2R_3+R_3R_1}{R_2}\) \(r_2 = \frac {R_1R_2+R_2R_3+R_3R_1}{R_3}\) \(r_3 = \frac {R_1R_2+R_2R_3+R_3R_1}{R_1}\)
電力
電力:電気製品を使用するときに1秒あたりに消費される電気エネルギー。
$$\Large{P = VI}$$
\(P\)[W(=J/s)]:電力 \(V\)[V]:電位差
電力量
電力量:電気製品を使用するときに消費される総電気エネルギー。
$$\Large{W = Pt}$$
\(W\)[J]:電力量 \(P\)[W]:電力 \(t\)[s]:時間


