理論その2 静電気(Static Electricity)

このページでは、静電気の公式や重要単語とその解説について掲載しています。
また、その公式がどの過去問に使われているかについても記載しています。
静電気の分野では、電荷周りの電界の強さや電界中の静電力、コンデンサの計算問題が中心に出題されます。
公式を使うことができれば取れる問題が多く、また出題数も比較的多いため点数を取りやすい分野といえます。
クーロンの法則
静電力は2つの電荷量の積に比例し、距離の2乗に反比例する。
$$\Large{F = k\frac {|Q_1||Q_2|}{r^2}}$$
\(k\):比例定数
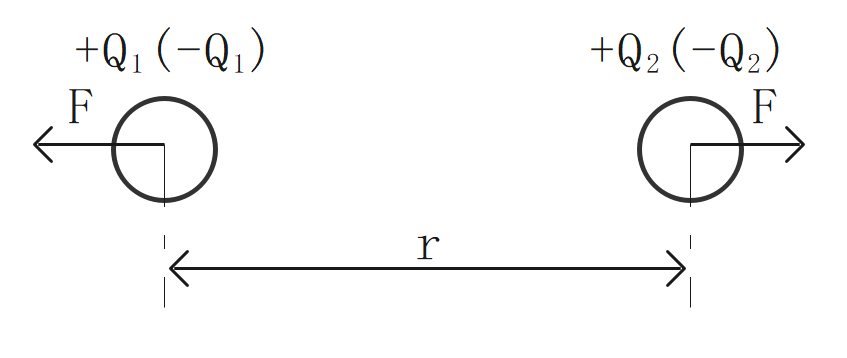
電荷の平均化
大きさの等しい2つの導体球を接触させると、両方の導体球に蓄えられている電荷が平均される。
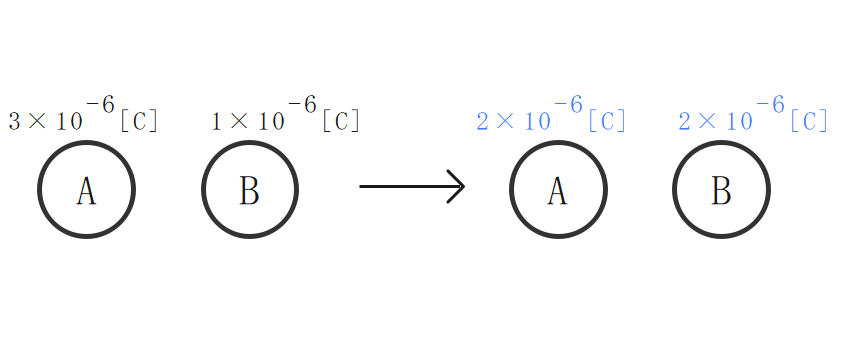
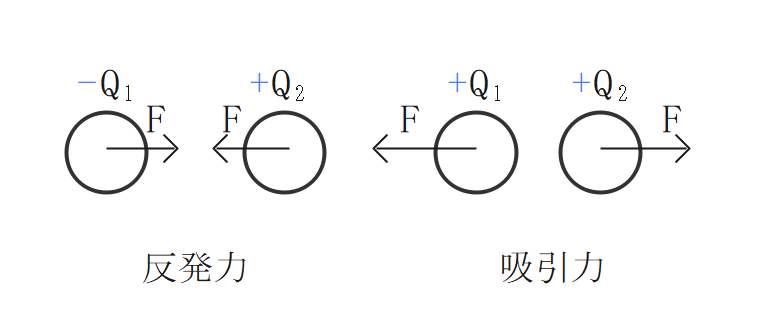
吸引力と反発力(斥力)
2つの電荷が別符号の場合、電荷間には吸引力が働く。
2つの電荷が同符号の場合、電荷間には反発力(斥力)が働く。
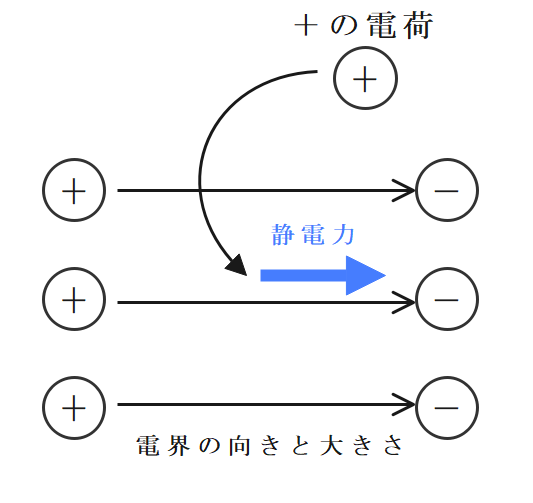
電界で働く静電力の大きさ
電界で働く静電力の大きさは、電荷量と電界の大きさの積に比例する。
$$\Large{F = QE}$$
\(F\):静電力[N] \(Q\):電荷[C] \(E\):電界の大きさ[V/m]
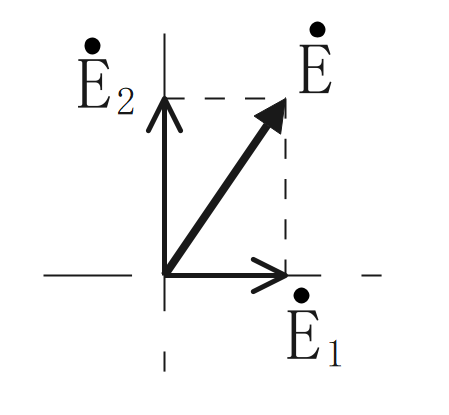
電界の大きさと向き
電界の大きさと向きは合成できる。
下図の場合、\(E_1\)と\(E_2\)が直交しているため、
$$E=\sqrt{E^2_1+E^2_2}$$
となる。
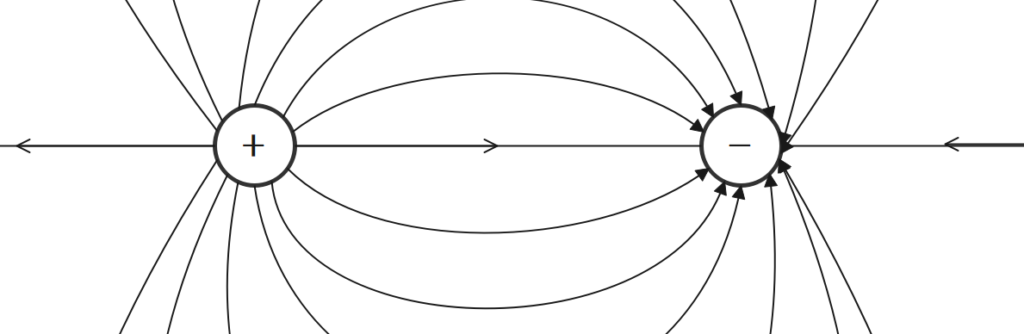
電気力線の性質
- 正電荷から負電荷に流れる架空の線。
- 電気力線は互いに交わったり、折れ曲がったり、消えたり、枝分かれしない。
- 電気力線の接線の向きが、電界の向きとなる。
- 導体表面に垂直に出入りし、導体内部には存在しない。
ガウスの法則(電気力線)
周囲の媒質が誘電率εである電荷+Q(-Q)からは、次の式の本数だけ電気力線が出る(入る)。
$$\Large{N = \frac {Q}{ε}}$$
\(N\):電気力線 \(Q\):電荷[C] \(ε\):誘電率[F/m]
電界の大きさ
電界の大きさは、単位面積当たりの電気力線の本数すなわち電気力線の密度を表す。
$$\Large{E = \frac {N}{A}=\frac {Q}{4πεr^2}}$$
\(E\):電界の大きさ[V/m] \(N\):電気力線 \(A\):表面積[m2] \(ε\):誘電率[F/m] (r\):球の半径[m]
上式と1.クーロンの法則より、
$$\Large{k = \frac {1}{4πε}}$$
\(k\):比例定数
電束密度
$$\Large{D = \frac {Ψ}{A}}$$
\(D\):電束密度[C/m2] \(Ψ\):電束[C] \(A\):断面積[m2]
電束密度と電界の大きさの関係式
電束密度は電界の大きさと誘電率の積に比例する。
$$\Large{D = εE=ε_0ε_rE}$$
\(D\):電束密度[C/m2] \(ε\):誘電率[F/m] \(ε_0\):真空中の誘電率[F/m] \(ε_r\):比誘電率
\(E\):電界の大きさ[V/m]
電位による仕事
一様な電界中Eで、点電荷Qをlだけ動かしたときの仕事Wを表す。
$$\Large{W = QV=QEl}$$
\(W\):エネルギー[J] \(Q\):電荷[C] \(V\):電位[V] \(E\):電界の大きさ[V/m] \(l\):移動させた距離[m]
電荷周りの電位
点電荷Qからr[m]離れた点Pの電位を求める公式
$$\Large{V = \frac {Q}{4πεr}}$$
\(V\):電位[V] \(Q\):電荷[C] \(ε\):誘電率[F/m] \(r\):点電荷から点Pまでの距離[m]
コンデンサに蓄えれる電荷
コンデンサに蓄えられる電荷量は、静電容量と極板間の電位差の積に比例する。
$$\Large{Q = CV=DA}$$
\(Q\):電荷[C] \(C\):静電容量[F] \(V\):極板間の電位差[V] \(D\):電束密度[C/m2] \(A\):極板の面積[m2]
平行平板コンデンサの静電容量
静電容量は、誘電率と極板の面積の積に比例し、極板間の距離に反比例する。
$$\Large{C = \frac {εA}{l}}$$
\(Q\):電荷[C] \(ε\):誘電率[F/m]
\(A\):極板の面積[m2] \(l\):極板間の距離[m]
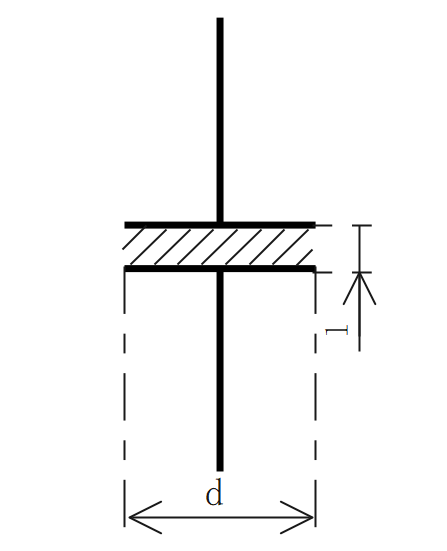
平行平板コンデンサの電界の大きさ
平行平板コンデンサの電界の大きさは、極板間の電位差に比例し、極板間の距離に反比例する。
$$\Large{E = \frac {V}{l}}$$
\(E\):電界の大きさ[V/m] \(V\):電位[V] \(l\):コンデンサの幅[m]
平行平板コンデンサの等電位面
平行板コンデンサ内(誘電体内)は電界が一様に発生しているため,平行板コンデンサ内(誘電体内)の等電位面は電極板と平行になる。
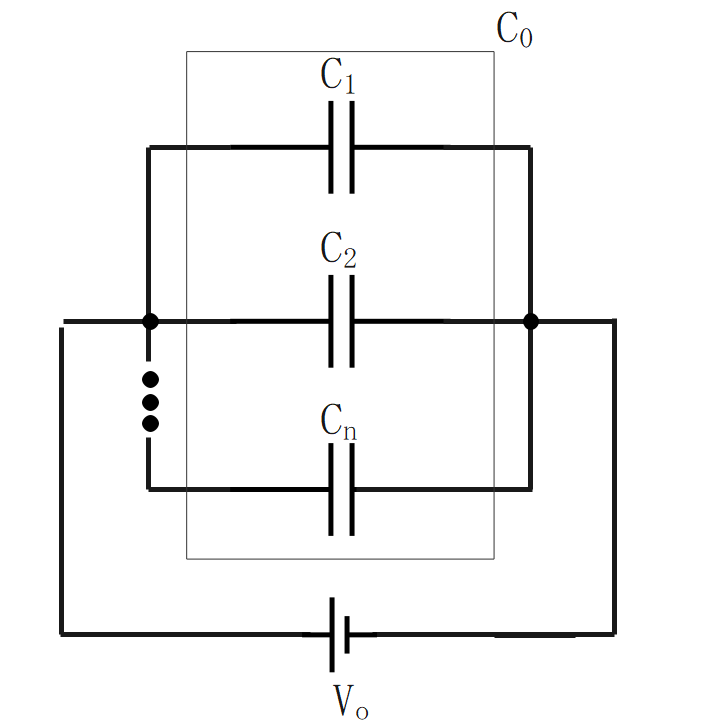
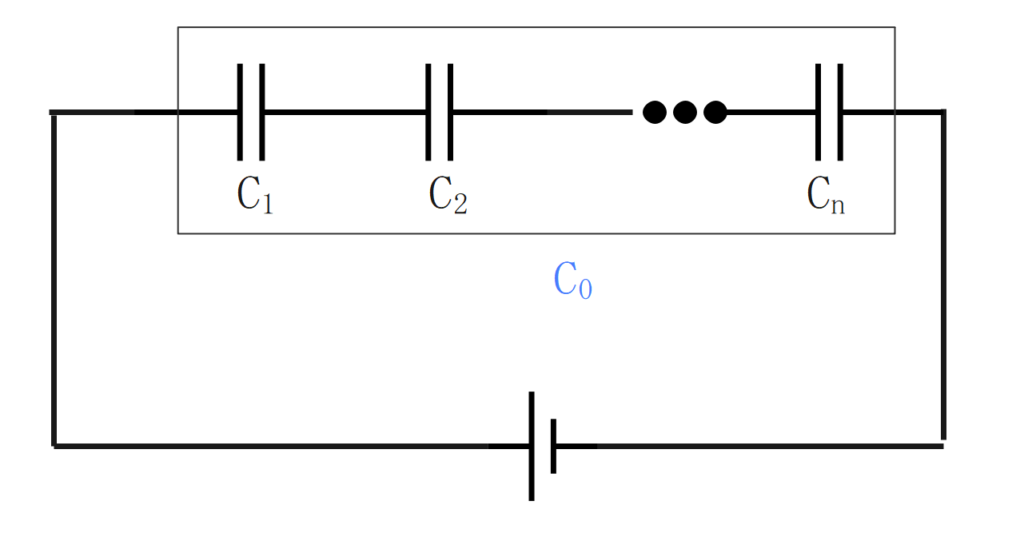
コンデンサの並列接続
合成静電容量
並列接続の合成静電容量は、各コンデンサの静電容量の和となる。
$$\Large{C_o = C_1+C_2+\cdots+C_n}$$
\(C_o\):合成静電容量[F] \(C_n\):各静電容量[F]
全電荷量
並列接続の全電荷量は、各コンデンサに蓄えられた電荷量の和となる。
$$\Large{Q_o = Q_1+Q_2+\cdots+Q_n}$$
\(C_o\):全電荷量[C] \(C_n\):各電荷量[C]
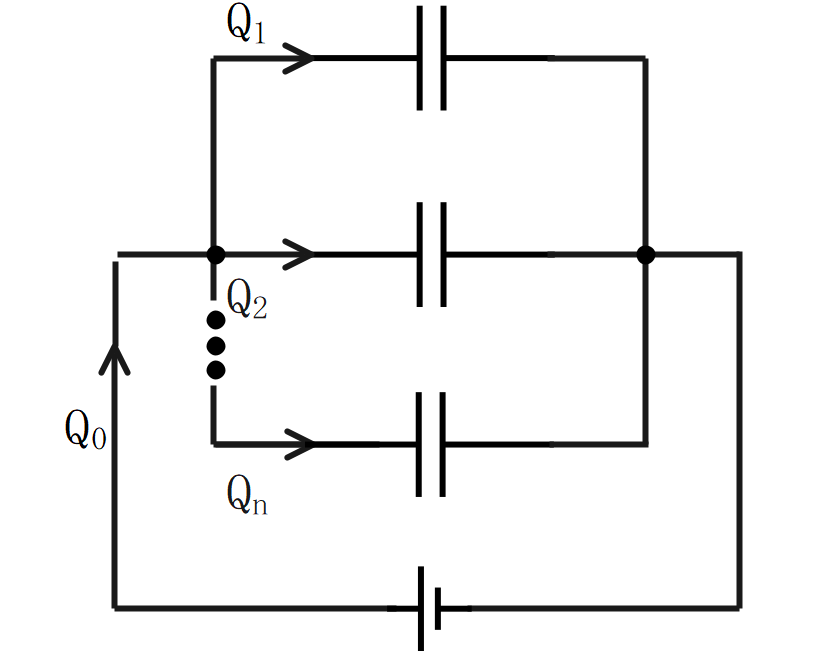
全電圧
並列接続の全電圧は、各コンデンサの電位差と等しくなる。
$$\Large{E_o = V_1=V_2=…=V_n}$$
\(E_o\):全電圧[V] \(V_n\):各電圧[V]
分流
各コンデンサに流れる電流は、求める電荷量の静電容量に比例し、各コンデンサの静電容量の和に反比例する。
$$\Large{Q_1 = Q×\frac{C_1}{C_1+C_2}}$$
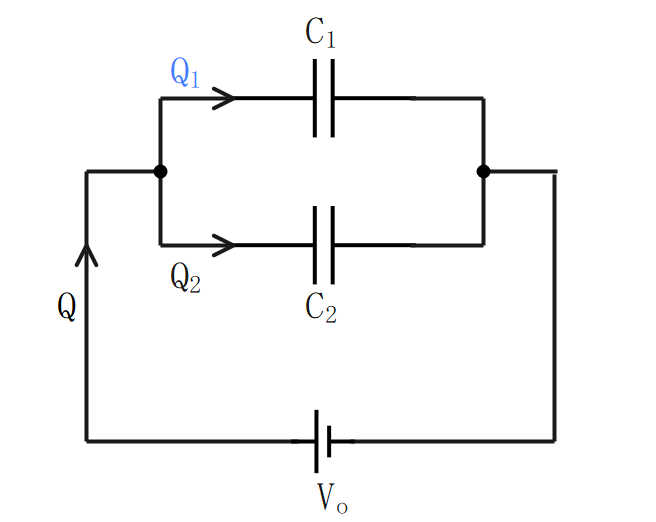
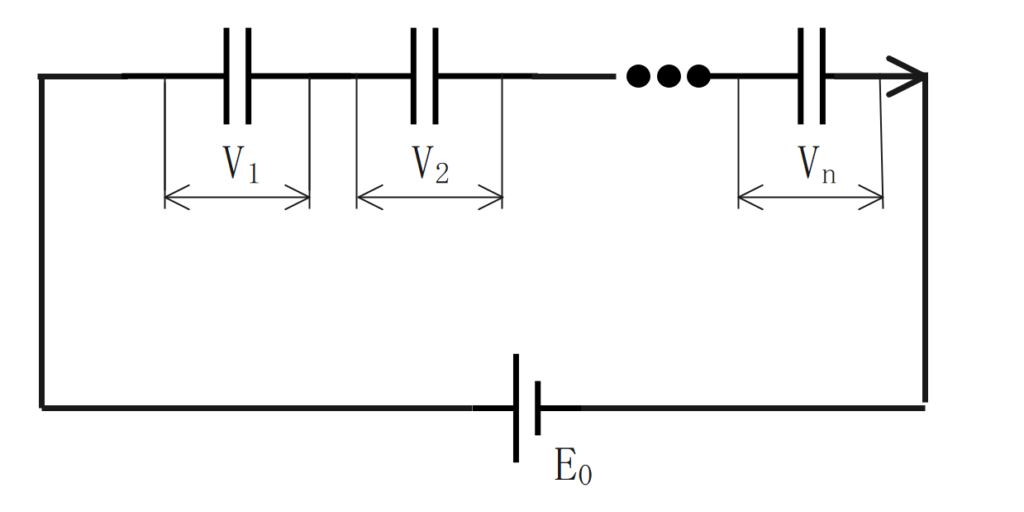
コンデンサの直列接続
合成静電容量
直列接続の合成静電容量は、各コンデンサの静電容量の逆数の和の逆数となる。
$$\Large{C_o = \frac {1}{\frac {1}{C_1}+\frac {1}{C_2}+\cdots+\frac {1}{C_n}}}$$
\(C_o\):合成静電容量[F] \(C_n\):各静電容量[F]
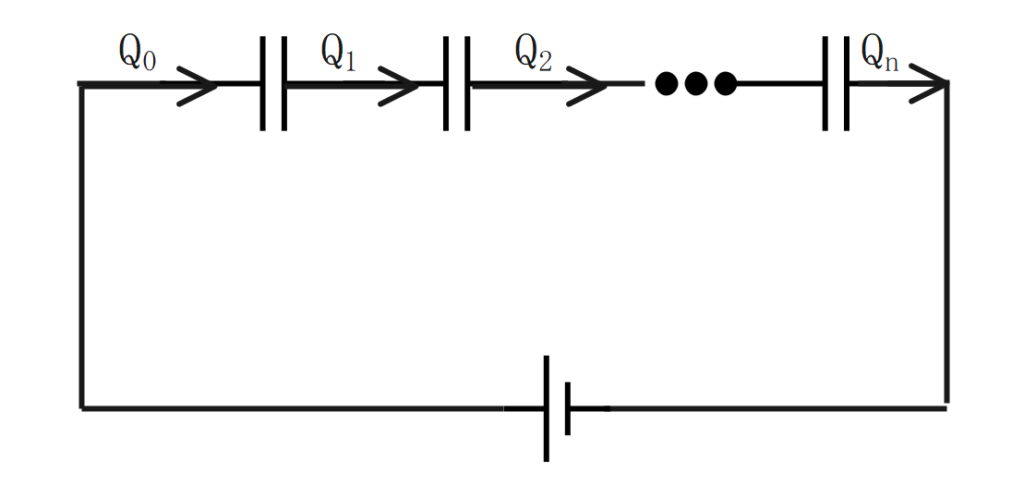
全電荷量
並列接続の全電荷量は、各コンデンサに蓄えられた電荷量と等しくなる。
$$\Large{Q_o = Q_1=Q_2=\cdots=Q_n}$$
\(C_o\):全電荷量[C] \(C_n\):各静電容量[C]
全電圧
並列接続の全電荷量は、各コンデンサの電位差の和になる。
$$\Large{E_o = V_1+V_2+\cdots+V_n}$$
\(E_o\):全電圧[V] \(V_n\):各電圧[V]
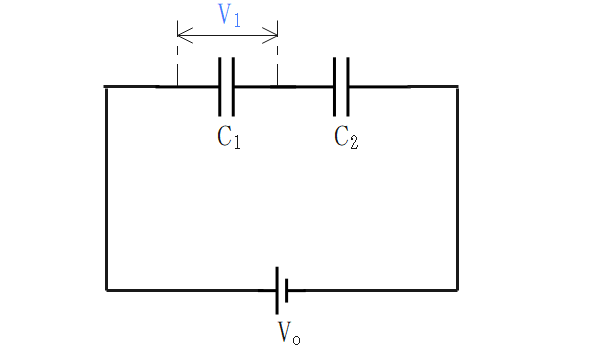
分圧
各コンデンサに流れる電流は、求める電荷量と逆の静電容量に比例し、各コンデンサの静電容量の和に反比例する。
$$\Large{V_1 = V_0×\frac {C_2}{C_1+C_2}}$$
静電エネルギー
静電エネルギーは、静電容量と極板間の電位差の2乗の積に比例する。
$$\Large{W = \frac {1}{2}CV^2}$$
\(W\):静電エネルギー[J] \(C\):静電容量[F] \(V\):電圧[V]


