機械その1 直流機(DC Machine)

このページでは、直流機の公式や重要単語とその解説について掲載しています。
また、その公式がどの過去問に使われているかについても記載しています。
直流機の分野では、直流機の特性や分類を問う知識問題や直流機で生じる電流の計算問題が中心に出題されます。
また、出題される問題はパターン化されているものが多いため、過去問を繰返し解いて慣れておくと良いでしょう。
誘導起電力
誘導起電力の求め方
$$E = Blvsinθ = \frac{pZ}{60a}ΦNsinθ
= K_1ΦNsinθ$$
\(E\):誘導起電力[V] \(B\):磁束密度[T] \(l\):電線の長さ[m] \(v\):運動の速度[m/s] \(θ\):運動の向きと磁束密度の向きの角度[°] \(p\):磁極数 \(Z\):電機子の導体数 \(φ\):磁束[Wb] \(K_1\):電圧定数※ \(N\):回転数[rpm]
※\(K_1=\frac{pZ}{60a}\)
電磁力
電磁力の求め方
$$\Large{F = BlIsinθ}$$
\(F\):電磁力[N] \(B\):磁束密度[T] \(l\):電線の長さ[m] \(I\):電流[A]
直流機の構造
固定子
- 界磁:電磁石となる部分(磁束を作る)
- 継鉄:界磁の外枠となる部分。
回転子
- 電機子:電機子鉄心と電機子巻線からなる。
⇒電機子鉄心には,交番磁束による渦電流損を少なくするため,電磁鋼板を層状に重ねた積層鉄心が用いられる。 - 整流子:交流を直流に変換する素子。
電機子巻線の巻き方
重ね巻(並列巻)
- 並列回路数a = 磁極数P
- 並列回路数a = ブラシの数
- 低電圧・高電流に適する。
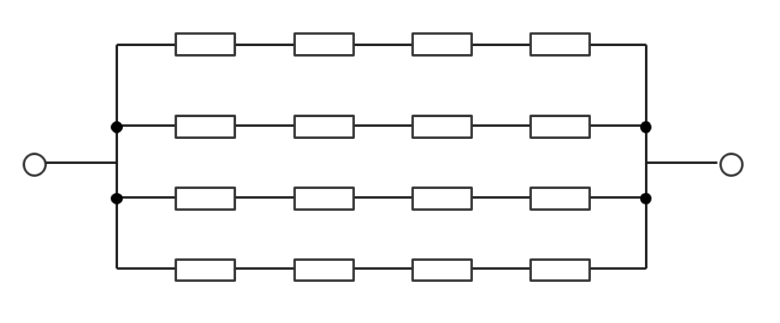
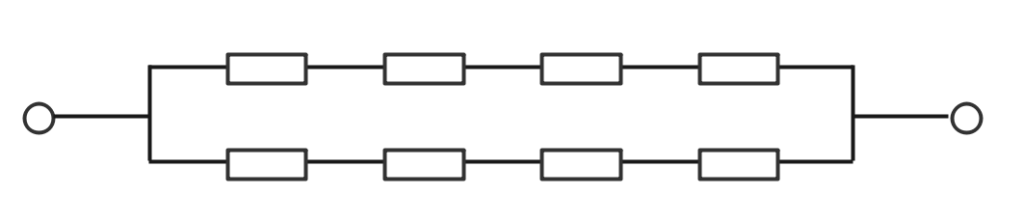
波巻(直列巻)
- 並列回路数a = 2
- 磁極数P = 2
- 高電圧・低電流に適する。
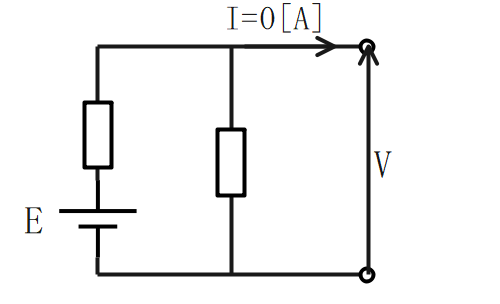
無負荷運転時の直流発電機の特性
電源電圧と端子電圧が等しくなる。
$$\Large{E = V}$$
電機子反作用
電機子巻線に電流が流れると、右ねじの法則により磁束が発生し、界磁巻線による主磁束に影響を与える。
⇔電機子電流による起磁力がエアギャップの磁束分布に影響を与える作用を電機子反作用という。
- 主磁束の減少 :主磁束が減少するため、誘導起電力も減少する。(\(e=\frac{pZ}{60a}ΦN\)より)
- 電気的中性軸の移動:起電力が生じたコイルをブラシで短絡してしまい、火花が発生する。
- 整流子片間の電力が不均一。
※対応策:補極巻線や補極を設ける。
⇒接続方法は発電機と電動機どちらも同じでよい。
直流機の分類
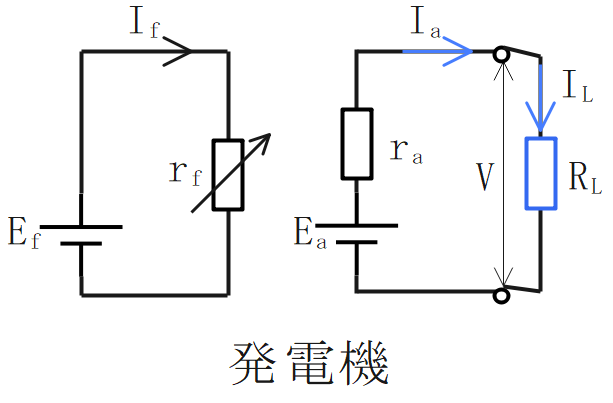
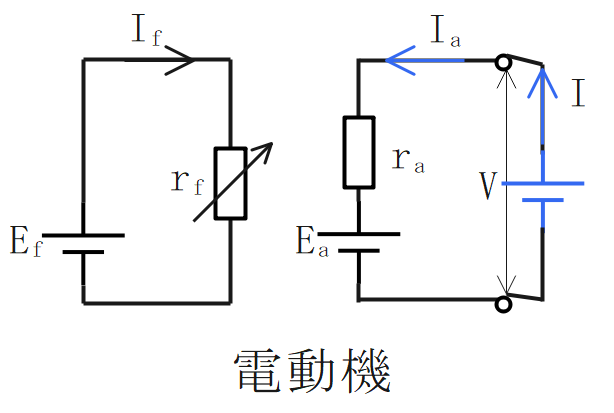
他励式:界磁回路と電機子回路が分離されている。
発電機
端子電圧は、起電力と電機子抵抗、電機子電流の積の差に比例する。
$$\Large{V = E_a-r_aI_a}$$
界磁電流は、外部の電源電圧に比例し、界磁抵抗に反比例する。
$$\Large{I_f = \frac{E_f}{r_f}}$$
電機子電流と負荷電流は等しくなる。
$$\Large{I_a=I_L}$$
電動機
起電力は、端子電圧と電機子抵抗、電機子電流の積の差に比例する。
$$\Large{E_a = V-r_aI_a}$$
界磁電流は、電源電圧に比例し、界磁抵抗に反比例する。
$$\Large{I_f = \frac{E_f}{r_f}}$$
電機子電流と負荷電流は等しくなる。
$$\Large{I_a=I}$$
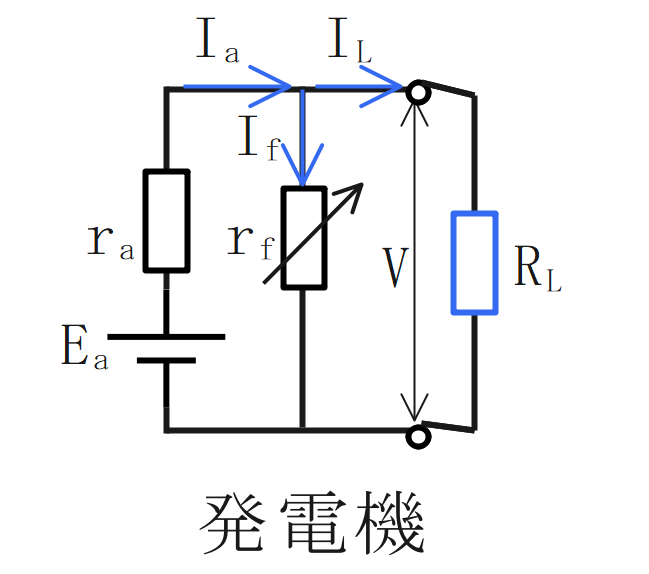
分巻式:界磁回路と電機子回路が並列接続されている。
発電機
端子電圧は、起電力と電機子抵抗、電機子電流の積の差に比例する。
$$\Large{V = E_a-r_aI_a}$$
界磁電流は、端子電圧に比例し、界磁抵抗に反比例する。
$$\Large{I_f = \frac{V}{r_f}}$$
電機子電流は、界磁電流と負荷電流の和に比例する。
$$\Large{I_a=I_f+I_L}$$
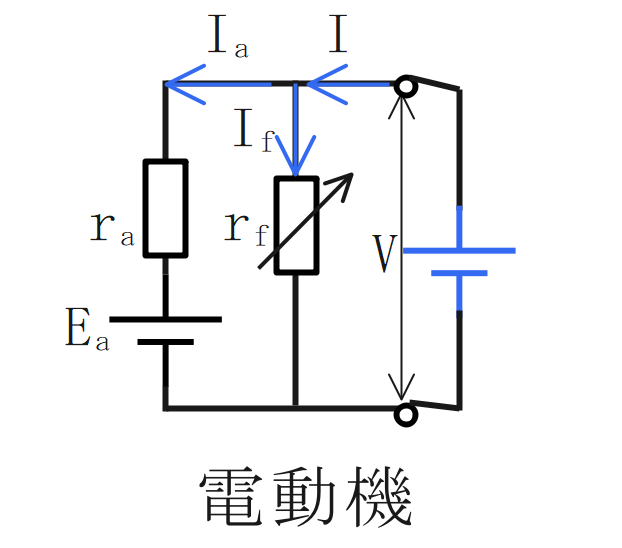
電動機
起電力は、端子電圧と電機子抵抗、電機子電流の差に比例する。
$$\Large{E_a = V-r_aI_a}$$
界磁電流は、端子電圧に比例し、電機子抵抗に反比例する。
$$\Large{I_f = \frac{V}{r_f}}$$
負荷電流は、界磁電流と電機子電流の和に比例する。
$$\Large{I=I_f+I_a}$$
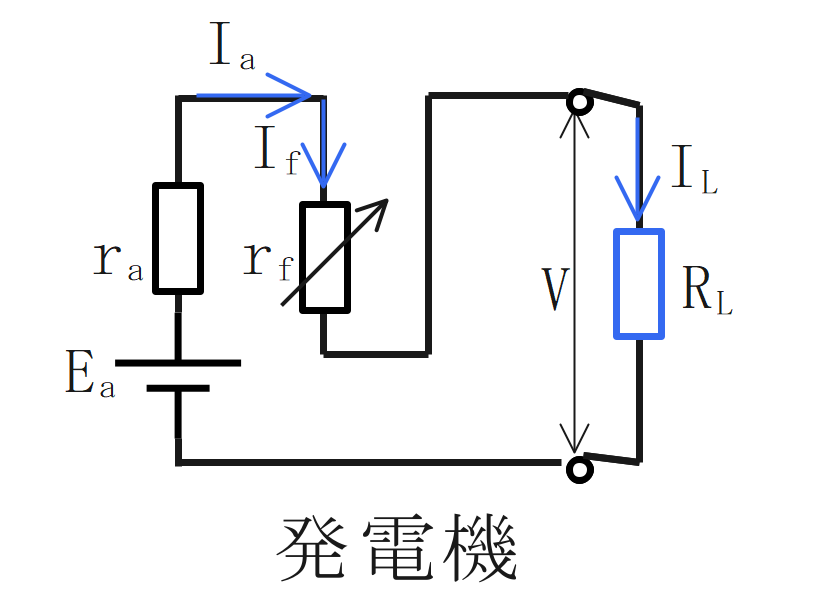
直巻式:界磁回路と電機子回路が直列接続されている。
発電機
負荷電流は、界磁電流と電機子電流の和に比例する。
$$\Large{V = E_a-(r_a+r_f)I_a}$$
電機子電流と界磁電流と負荷電流が等しくなる。
$$\Large{I_a=I_f=I_L}$$
電動機
起電力は、端子電圧と電機子電流の積に比例する。
$$\Large{E_a = V(r_a+r_f)Ia}$$
界磁電流は、端子電圧に比例し、界磁抵抗に反比例する。
$$\Large{I_f = \frac{V}{r_f}}$$
電機子電流と界磁電流と負荷電流が等しくなる。
$$\Large{I_a=I_f=I}$$
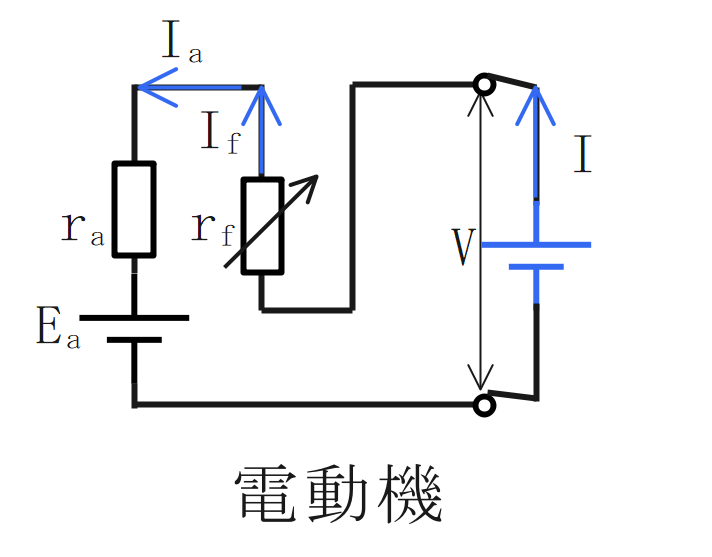
直流電動機のトルク
トルクは、磁束と電機子電流の積に比例する。
$$\Large{T = \frac{pZ}{2πa}ΦI_a=K_2ΦI_a}$$
\(T\):トルク[N] \(p\):磁極数 \(Z\):電機子の導体数 \(α\):並列接続数 \(φ\):磁束[Wb]
直流電動機の出力
直流電動機の出力は、回転速度とトルクの積に比例する。
$$\Large{P_o=ωT=\frac{2πN}{60}T=E_aI_a}$$
\(ω\):角速度[rad/s] \(T\):トルク[N] \(N\):回転数[rpm]
直流電動機の特性
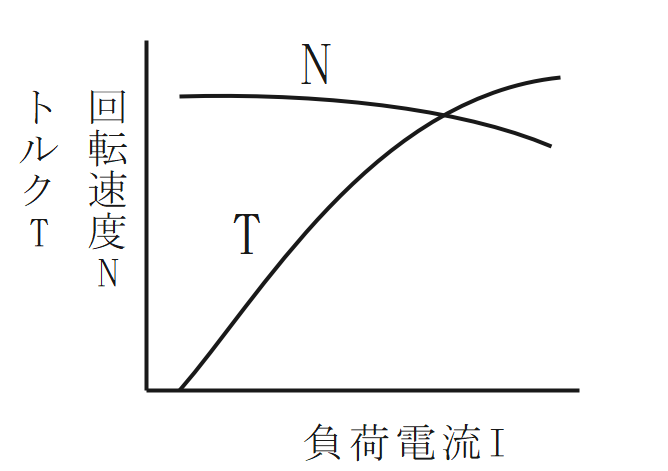
分巻式
- 回転速度はほぼ一定(定速度電動機)
⇒速度特性 - トルクは負荷電流に比例する。
⇒トルク特性
$$\Large{N=\frac{V-r_aI_a}{K_1Φ}=\frac{V-r_a(I-I_f)}{K_1Φ}}$$
$$\Large{T=K_2ΦI_a=K_2Φ(I-I_f)}$$
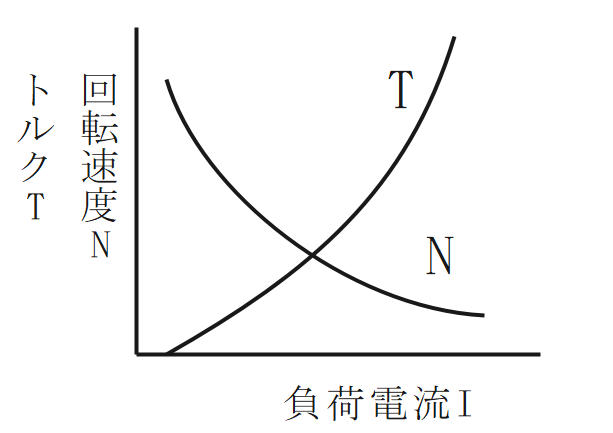
直巻式
- 回転速度は負荷電流に反比例する(変速度電動機)
⇒速度特性 - トルクは負荷電流に2乗に比例する。
⇒トルク特性
※ 直巻電動機は始動時に大きなトルクTが発生する。
$$\Large{N=\frac{V-(r_a+I_f)I_a}{K_1Φ}=\frac{VR_m}{K_1NI}-\frac{r_a+r_f}{K_1N}}$$
$$\Large{T=K_2ΦI_a=K_2\frac{NI^2}{R_m}}$$
他励式
- 電圧制御と界磁制御により、広い範囲で速度を制御できる。
⇒圧延機の駆動などに使われる。
始動電流
- 直流電動機は、始動時は電機子が回転していないため、逆起電力Eaが0になる。
また、電機子抵抗raも小さいため、非常に大きな電流Ia(始動電流)が流れる。
⇒電機子巻線を焼損する。
※対応策:始動抵抗を設けて抵抗を大きくする。
$$\Large{I_a=\frac{V}{r_a}}$$
直流電動機の速度制御
- 電圧制御
- 抵抗制御:可変抵抗を電機子と直列に接続する。
- 界磁制御:界磁電流Ifを変化させる。
$$\Large{N=\frac{V-r_aI_a}{K_1Φ}}$$
その他の特性
- 分巻発電機は、始動時に界磁の残留磁束によって低い電圧で発電が始まり、徐々に電圧が上昇する。
- 直巻発電機は、界磁電極が磁気飽和すると、出力電圧Vは安定する。
- ブラシレスDCモータは、界磁電界に同期して永久磁石の開示が回転する
⇒すべり0(同期機)
直流機の効率
$$\Large{η=\frac{P_{out}}{P_{out}+P_c+P_i}×100}$$
\(P_{out}\):出力[W] \(P_c\):銅損[W] \(P_i\):鉄損[W]
※銅損:電流が流れたときに生じる。
鉄損:何もしなくても常に生じている。
⇒ヒステリシス損(周波数に比例)や渦電流損(鉄心の抵抗)


