電力その2 火力発電(Thermal power)

このページでは、火力発電の公式や重要単語とその解説について掲載しています。
また、その公式がどの過去問に使われているかについても記載しています。
水力発電の分野では、水力発電所の特徴や水車の種類を問う知識問題や、ベルヌーイの定理を用いた計算問題が中心に出題されます。
出題される問題はパターン化されているものが多いため、過去問を繰返し解いて慣れておくと良いです。
ボイラの主な設備
空気予熱器
- 空気を煙道を通る燃焼ガスによって加熱する。
ドラム
- 水分と飽和蒸気を分離するほか、蒸発管への送水を行う。
過熱器
- 飽和蒸気を乾燥した蒸気にする。
節炭器
- 煙道に給水ルートを通し、給水を加熱する。
再熱器
- 高圧タービンで仕事をした蒸気を加熱し、低圧タービンに送る。
タービンの種類
復水タービン
- タービンの出口蒸気を復水器で水にする。真空度が高まり、回転力を高める。
再熱タービン
- ボイラの再熱器を通す機構のタービン
再生タービン
- タービンの中間から上記の一部を取り出して、その蒸気で給水を加熱する。
タービン発電機の特徴
- 磁極数が少ないため、回転速度が高くなる。
- 機械的強度が必要である。
・円筒形
・直径を小さくし、軸方向に長くする。
復水器
- エネルギー損失が最も大きい。
- 冷却水の温度が低いほど、復水器の真空度は高くなる。
- 真空度が高くなるほど、タービンで蒸気が膨張して回転力が上がる。
ランキンサイクル
汽力発電の基本的な熱サイクル。
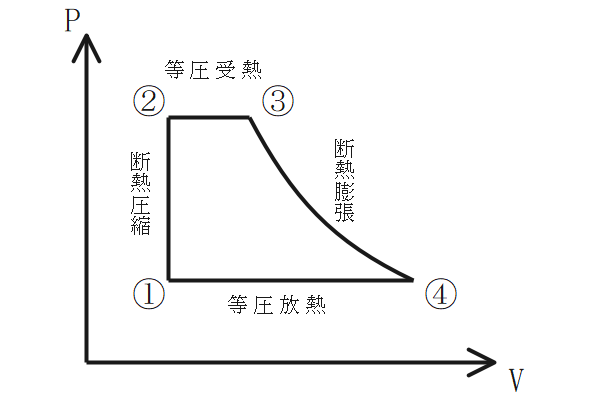
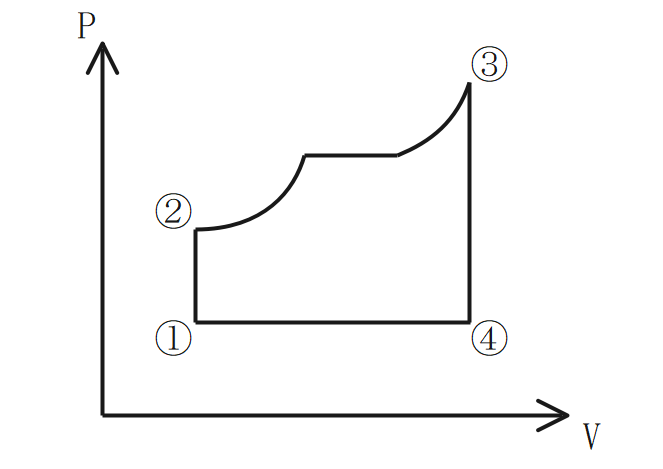
- ①→②:給水ポンプで水に圧力を掛ける。
- ②→③:ボイラや過熱器で過熱し水を蒸気にする。
- ③→④:蒸気タービン内で仕事をしている状態。
- ④→①:復水器で蒸気を水にする。
※エントロピーs:熱を受け取る→「+」、熱を放出する「-」
発電端出力
$$\Large{P_G = P_L+P_S}$$
\(P_G\):発電端出力[W] \(P_L\):所内電力[W] \(P_S\):送電端出力[W]
$$\Large{L = \frac{P_L}{P_G}×100}$$
\(L\):所内率[%] \(P_G\):発電端電力[W] \(P_L\):所内電力[W]
復水器の持ち去る熱量
$$\Large{Q = qcρΔT}$$
\(Q\):熱量[J] \(q\):流量[m^3/h] \(c\):比熱 \(ρ\):液体の密度[kg/m^3] ΔT[]:入口温度と出口温度の差
コンバインドサイクル発電
- 圧縮機→燃焼器→ガスタービン→排熱回収ボイラ
- 排ガス量は多い。
- 出力分担が小さいため、復水器の冷却水量は少なくても良い。
- 小型の所内補機が多いため、所内率は小さい。
- 外気温が低いほど最大出力が増加する。
- 起動・停止時間が短い。
- 熱効率が高い。
高効率化の方法
・ガスタービンの入口温度を高くする。
・圧縮機の入口・出口の圧力比を増加させる。
各効率
ボイラ効率
$$\Large{η_B = \frac{Z(h_S-h_W)}{BH}×100}$$
\(η_B\):ボイラー効率[%] \(Z\):蒸気量[kg\h] \(h_S\):蒸気の比エンタルピー[kJ/kg] \(h_W\):給水の比エンタルピー[kJ/kg] \(B\):発熱量[kJ/kg] \(H\):燃料消費量[kg/h]
タービン効率
$$\Large{η_t = \frac{3600P_t}{Z(h_S-H_t)}×100}$$
\(η_t\):タービン効率[%] \(P_t\):タービン出力[W] \(Z\):蒸気量[kg\h] \(h_S\):蒸気の比エンタルピー[kJ/kg] \(h_t\):タービン排気の比エンタルピー[kJ/kg]
発電機効率
発電機入口出力と出口出力の比
$$\Large{η_g = \frac{P_G}{P_t}×100}$$
\(η_g\):発電機効率[%] \(P_G\):発電機出力[W] \(P_t\):タービン出力[%]
ランキンサイクルの熱効率
$$\Large{η_R = \frac{h_S-h_t}{h_S-h_W}}$$
\(η_R\):ランキンサイクルの熱効率 \(h_S\):蒸気の比エンタルピー[kJ/kg] \(h_t\):タービン排気の比エンタルピー[kJ/kg] \(h_W\):給水の比エンタルピー[kJ/kg]
コンバインドサイクルの熱効率
$$\Large{η_C = η_g+η_S(1-η_g)}$$
\(η_C\):コンバインドサイクルの熱効率 \(η_g\):発電機効率 \(η_S\):蒸気タービン効率


