電力その12 電線のたわみ(Deflection of Electric Wire)

このページについて
このページでは、電線のたわみの公式や重要単語とその解説について掲載しています。
また、その公式がどの過去問に使われているかについても記載しています。
線路計算のポイント
電線のたわみの分野では、電線のたわみや張力を求める計算問題が中心に出題されます。
出題数は少ないため、重要度は低いですが、簡単に解ける問題が多いため勉強しておきましょう。
目次
電線のたわみ
公式
$$\Large{D=\frac{WS^2}{8T}}$$
\(D\):電線のたるみ[m] \(W\):電線1m当たりの荷重[N/m] \(S\):径間[m] \(T\):水平張力[N]
電線の実長
公式
$$\Large{L=S+\frac{8D^2}{3S}}$$
\(L\):電線の実長[m] \(S\):径間[m] \(D\):電線のたるみ[m]
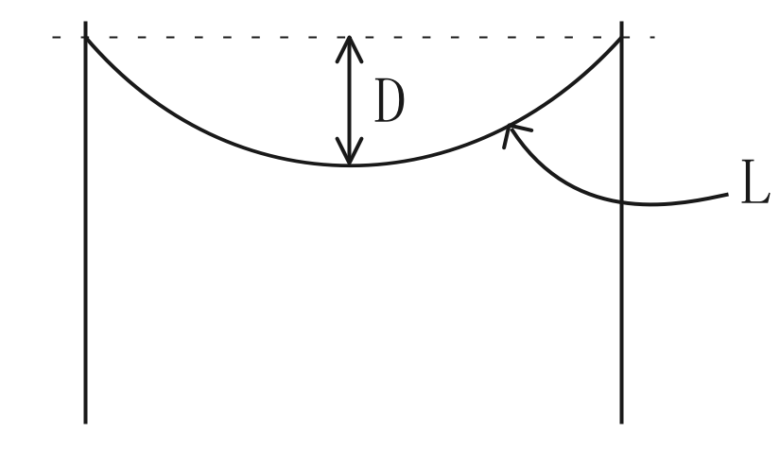
温度変化後の実長
公式
$$\Large{L_2=L_1(1+α(t_2-t_1))}$$
\(L_2\):温度変化後の実長[m] \(L_1\):温度変化前の実長[m] \(α\):電線の線膨張係数 \(t_2\):温度変化後の温度[℃] \(t_1\):温度変化前の温度[℃]
電線の水平張力
公式
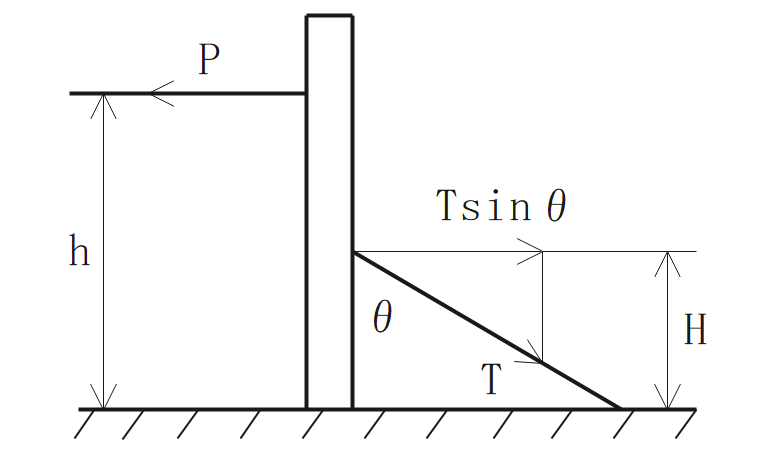
$$\Large{P=Tsinθ}$$
\(P\):水平張力(電線張力)[N] \(T\):支線を支える張力[N] \(θ\):電柱と支線の角度[°]
モーメントのつり合い
公式
$$\Large{Ph=Thsinθ}$$
\(P\):水平張力(電線張力)[N] \(h\):電柱の電線の高さ[m] \(T\):支線を支える張力[N] \(θ\):電柱と支線の角度[°]
あわせて読みたい


機械その1 直流機(DC Machine)
このページについて このページでは、直流機の公式や重要単語とその解説について掲載しています。また、その公式がどの過去問に使われているかについても記載しています...

