理論その６ 過渡現象(Transient Phenomenon)
このページでは、過渡現象の公式や重要単語とその解説について掲載しています。
また、その公式がどの過去問に使われているかについても記載しています。
過渡現象の分野では、波高率、波形率の計算問題や抵抗とリアクタンスの組合せによる初期値、定常値の知識問題が中心に出題されます。
覚えていれば解ける簡単な問題が比較的多いため、点数の取りやすい分野ともいえます。
非正弦波交流の瞬時値
高調波成分により、乱れが生じる。
$$\Large{v = V_O+\sqrt{2}V_1sin(ωt+Φ_1)+\sqrt{2}V_2sin(2ωt+Φ_2)+…\\＋\sqrt{2}V_nsin(nωt+Φ_n)}$$
\(V_O\)：直流成分 \(\sqrt{2}V_1sin(ωt+Φ_1)\)：基本波成分
\(\sqrt{2}V_2sin(2ωt+Φ_2)+…＋\sqrt{2}V_nsin(nωt+Φ_n)\)：高調波成分
$$\Large{i = I_O+\sqrt{2}I_1sin(ωt+Φ_1)+\sqrt{2}I_2sin(2ωt+Φ_2)+…\\＋\sqrt{2}I_nsin(nωt+Φ_n)}$$
\(I_O\)：直流成分 \(\sqrt{2}I_1sin(ωt+Φ_1)\)：基本波成分
\(\sqrt{2}I_2sin(2ωt+Φ_2)+…＋\sqrt{2}I_nsin(nωt+Φ_n)\)：高調波成分
非正弦波交流の実効値
$$\Large{V = \sqrt{V^2_0+V^2_1+V^2_2+…+V^2_n}}$$
非正弦波交流のひずみ率
ひずみ率は波形がどのぐらいひずんでいるかを割合にしたもの
$$\Large{k = \frac{\sqrt{V^2_2+V^2_3+…+V^2_n}}{V_1}×100}$$
\(k\)：ひずみ率
波高率
実効値に対する最大値の比。
$$\Large{\mathbf{波高率=\frac{最大値}{実効値}}}$$
波形率
平均値に対する実効値の比。
$$\Large{\mathbf{波形率=\frac{実効値}{平均値}}}$$
初期値と定常値
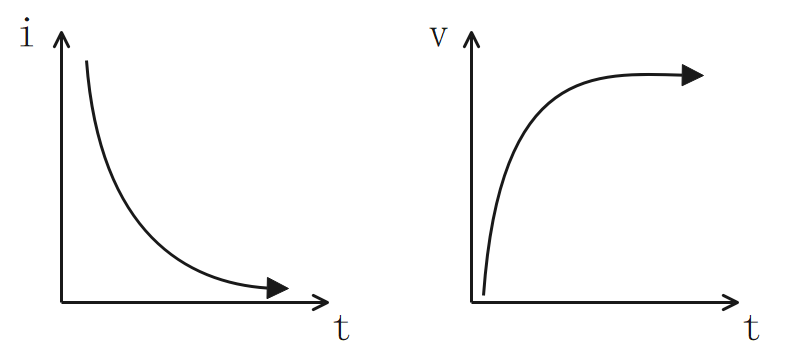
R-C回路
- 初期値：Cを短絡して計算する(Cに電流が流れる)
- 定常値：Cを開放して計算する(Cに電流が流れない)
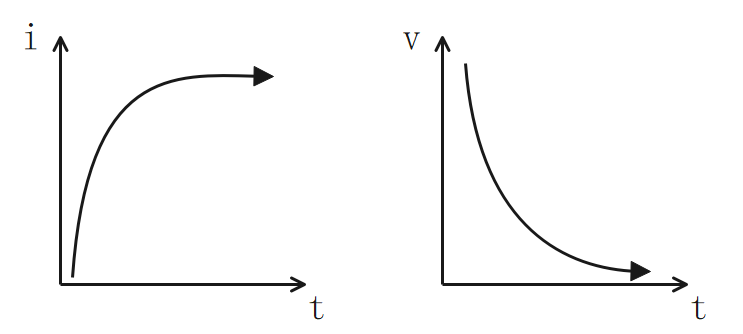
R-L回路
- 初期値：Lを開放して計算する(Lに電流が流れない)
- 定常値：Lを短絡して計算する(Lに電流が流れる)
時定数
- 時定数は、平衡状態(定常値)に達するまでの時間を表しており、電気回路における緩和時間のことを指す。
R-C回路
$$\Large{τ = RC}$$
\(τ\)：時定数[s] \(R\)：抵抗[Ω] \(C\)：静電容量[F]
R-L回路
$$\Large{τ = \frac{L}{R}}$$
\(τ\)：時定数[s] \(R\)：抵抗[Ω] \(L\)：インダクタンス[H]
この記事が気に入ったら
いいねしてね！