機械その３　誘導機(Induction Machine)

誘導電動機の原理

• 磁界中(固定子)を導体(回転子)が移動することで、誘導起電力が生じて渦電流が発生する。(右手の法則)

• 渦電流が磁界中を流れるため、電磁力が発生する。 (左手の法則)
  ※磁界を作る固定子は永久磁石ではなく、コイルに三相交流電流を流して電磁石にする。
  ⇒交流電流を流すため磁界は回転する(回転磁界)
  固定子：外側、回転子：内側

同期速度

 回転磁界の回転数は、周波数に比例し磁極数に反比例する。

三相誘導電動機の構造

かご形回転子

• 回転子両端を端絡環で電気的に接続している(定速度電動機)
• 構造が単純、頑丈、コンパクト。

巻線形回転子

• スリップリング・ブラシを接続して、外部の端子(外部抵抗)を接続できる。
• 外部抵抗(可変抵抗器R)を接続して、始動特性の改善や回転速度の制御が行える。

滑り

• s=0　　：\(N=N_S\)より、回転磁界が巻線を切らないためトルクT=0となる。
• 0＜s＜1：\(N＜N_S\)より、誘導起電力が生じてトルクTが発生する。⇒誘導電動機(運転中)
• s=1　 ：\(N=0\)より、回転子が停止しているが、回転磁界との相対速度により起電力が生じてトルクが発生するため、徐々に回転速度を上げる。

＊\(N＞N_S\)の場合、誘導発電機になる。

三相誘導発電機のパラメータ

二次誘導起電力

二次周波数(滑り周波数)

二次電流

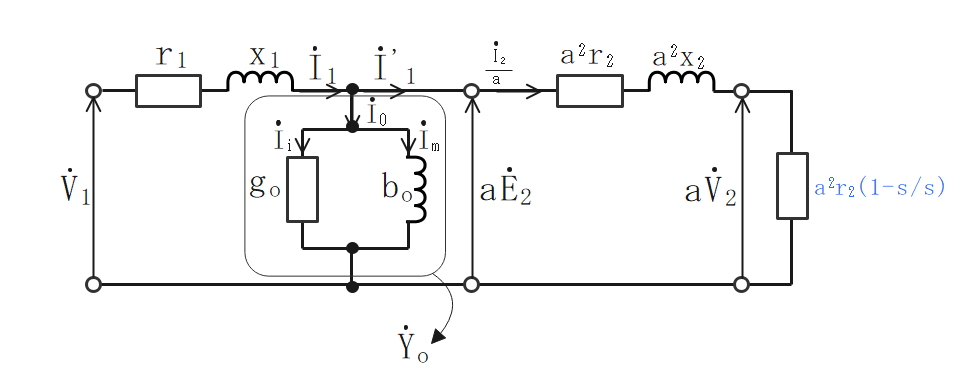
三相誘導電動機の等価回路(T形)

• 三相誘導電動機の回路を一次側に換算した等価回路(T形)を以下に示す。

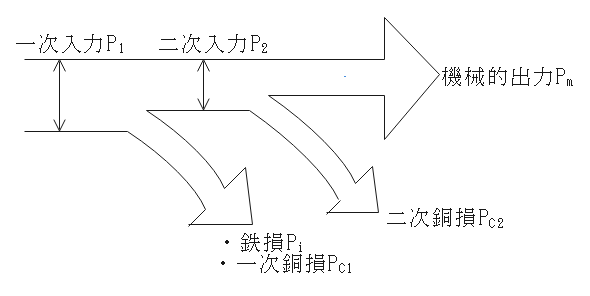
三相誘導電動機の熱勘定図

• 一次入力から機械的出力までの過程を以下に示す。

一次負荷電流

二次入力

三相分の二次入力

誘導機の効率

※鉄損がある場合は分母に\(P_i\)を足す。

機械的出力(定格出力)

トルク

滑り－トルク特性

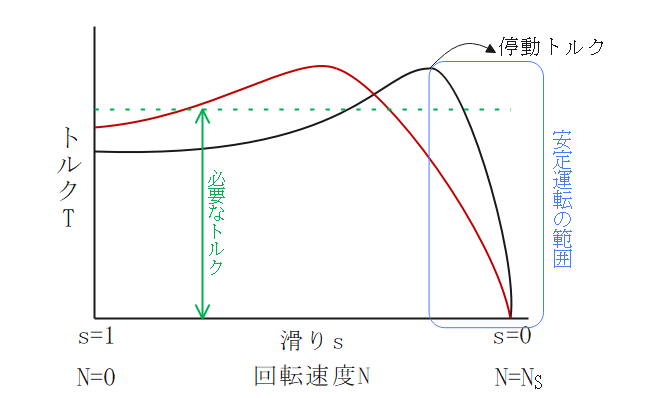
一定のトルクを得るための条件

三相誘導電動機の始動法

• 三相誘導電動機は始動電流が過大で始動トルクが過小であるため、これらの対策が必要である。
  対策を以下に示す。

かご形の始動法(1次回路を調整する)

• 全電圧始動法：停止している電動機に急に定格電圧を加える。
  　　　　　　　電動機出力が電源系統の容量に対して十分小さい場合に使える。
  　　　　　　　小型のモータに使用する。
• Y-△始動法：始動時に一次巻線をY結線とし、十分に加速した後、△結線にする。
  　　　　　　全電圧始動法に比べて、始動電流を\(\frac{1}{3}\)にできる。
  　　　　　　ただし、トルクも\(\frac{1}{3}\)になってしまう。
  　　　　　　5～15kWのモータに使用する。
• 始動補償器法：一次側に三相単巻変圧器を接続してタップ(巻数)を切り替えることで始動電圧下げる。15kW以上のモータに使用する。

巻線形の始動法(2次回路を調整する)

• 適当な大きさの外部抵抗に接続する(比例推移の性質を利用する)

三相誘導電動機の回転速度の制御法

かご形の速度制御

• 一次周波数制御法：VVVFインバータで周波数を制御する。
  ※\(\frac{V}{f}\)制御：電圧Vと周波数fの比を一定に保つ。(磁束も一定になる)
  　→トルクや効率の低下を防ぐ。
• 極数切替：極数を切り替える。
• 一次電圧制御

巻線形の速度制御

• 二次抵抗制御：外部抵抗による比例推移の性質を利用して、滑りsを変化させる。

その他

• 三相誘導電動機でRSTの内、2つ入れ替えて接続すると逆回転する。
  RSTの内、一本でも切れると回転しなくなる。
• 単相誘導電動機：始動トルクが0

あわせて読みたい

機械その４　同期機(Synchronous Machine) このページについて このページでは、同期機の公式や重要単語とその解説について掲載しています。また、その公式がどの過去問に使われているかについても記載しています...