機械その2 変圧器(Transformer)

このページでは、変圧器の公式や重要単語とその解説について掲載しています。
また、その公式がどの過去問に使われているかについても記載しています。
変圧器の分野では、変圧器の巻線抵抗や負荷損、無負荷損、短絡電流等を求める計算問題が中心に出題されます。似たような公式が多く、一見複雑に見えますが、慣れると簡単に解ける問題が多いので、過去問を繰返し解いて練習しましょう。
変圧器の特性
無負荷の変圧器の一次巻線に正弦波交流電圧を加えると,鉄心には磁気飽和現象やヒステリシス現象が生じるので電流は非正弦波電流となる。この電流を励磁電流といい,第 3 次をはじめとする多くの次数の高調波を含む。
変圧器の励磁電流のうち,一次電圧と同相成分を鉄損電流,\(\frac{π}{2}\)[rad]遅れた成分を磁化電流という。
変圧比、巻数比、電流比の関係
変圧器の変圧比と巻数比、電流比は一致する。
$$\Large{α=\frac{E_1}{E_2}=\frac{N_1}{N_2}=\frac{I_2}{I_1}}$$
\(E_1\):一次側の電源電圧[V] \(E_2\):二次側の電源電圧[V] \(N_1\):一次巻線 \(N_2\):二次巻線 \(I_1\):一次電流[A] \(I_2\):二次電流[A]
理想変圧器の等価回路
一次、二次巻線の抵抗、漏れ磁束、鉄損を無視した回路。
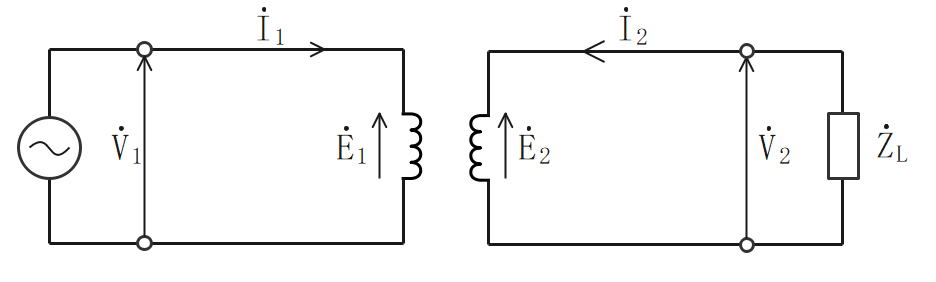
実際の変圧器の等価回路(T形)
二次側を一次側に変換した等価回路
発生する損失は鉄損に対応している。
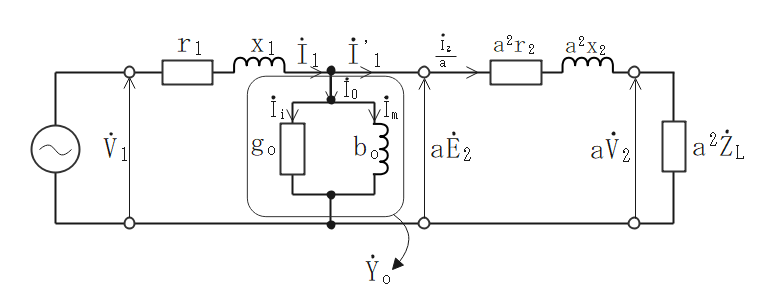
$$\Large{Y_o=g_o-jb_o}$$
\(Y_o\):励磁アドミタンス[S] \(g_o\):励磁コンダクタンス[S] \(Y_o\):励サセププタンス[S]
インピーダンス
$$\Large{Z=\sqrt{r^2+x^2}}$$
\(Z\):インピーダンス[Ω] \(r\):巻線の合成抵抗[Ω] \(x\):合成漏れリアクタンス[Ω]
$$\Large{r=r_1+α^2r_2}$$
\(r\):巻線の合成抵抗[Ω] \(r_1\):一次巻線の抵抗[Ω] \(a\):変圧比 \(r_2\):二次巻線の抵抗[Ω]
$$\Large{x=x_1+α^2x_2}$$
\(x\):合成漏れリアクタンス[Ω] \(r_1\):一次漏れリアクタンス[Ω] \(a\):変圧比 \(r_2\):二次漏れリアクタンス[Ω]
一次電圧の計算
$$\Large{V_1≒αV_2+r\frac{I_2}{α}cosθ+x\frac{I_2}{α}sinθ}$$
\(V_1\):一次電圧[V] \(a\):変圧比 \(V_2\):二次電圧[V] \(r\):巻線の合成抵抗[Ω] \(I_2\)二次電流[A] \(cosθ\):力率 \(x\):合成漏れリアクタンス[Ω]
電圧変動率
$$\Large{ε=\frac{V_{20}-V_{2n}}{V_{2n}}×100≒pcosθ+qsinθ}$$
\(ε\):電圧変動率[%] \(V_{20}\):無負荷時の二次電圧[V] \(V_{2n}\):定格時の二次電圧[V] \(V_{20}\):無負荷時の二次電圧[V] \(p\):百分率抵抗降下[%] \(cosθ\):力率 \(q\):百分率リアクタンス降下[%]
百分率抵抗降下
$$\Large{p=\frac{rI_{2n}}{V_{2n}}×100}$$
\(p\):百分率抵抗降下[%] \(r\):巻線の合成抵抗[Ω] \(I_{2n}\):定格時の二次電流[A] \(V_{2n}\):定格時の二次電圧[V]
百分率リアクタンス降下
$$\Large{q=\frac{xI_{2n}}{V_{2n}}×100}$$
\(q\):百分率リアクタンス降下[%] \(x\):合成漏れリアクタンス[Ω] \(I_{2n}\):定格時の二次電流[A] \(V_{2n}\):定格時の二次電圧[V]
定格容量
$$\Large{P_n=V_{1n}I_{1n}=V_{2n}I_{2n}}$$
\(P_n\):定格要領[W] \(V_{1n}\):定格時の一次電圧[V] \(I_{1n}\):定格時の一次電流[A] \(V_{2n}\):定格時の二次電圧[V] \(I_{2n}\):定格時の二次電流[A]
各損失
無負荷損と負荷損が等しくなった時、最大効率となる。
無負荷損
- 無負荷損=鉄損。
- 負荷電流に関わりなく一定。
- ヒステリシス損や渦電流損がある。
- ヒステリシス損は、周波数fに比例する。
渦電流損は、(f×t)の2乗に比例する。
負荷損
- 負荷損=銅損。
- 負荷電流の2乗に比例する。
$$\Large{P_C=RI^2}$$
\(P_C\):銅損[W] \(R\):抵抗[Ω] \(I\):電流[I]
無負荷試験
- 鉄損の測定
- 変圧器の二次側の負荷を開放し、一次側に定格電圧(インピーダンス電圧)を印加する。
短絡試験
- 銅損の測定
- 変圧器の二次側の負荷を短絡し、一次側に定格電圧(インピーダンス電圧)を印加する。
- 定格容量の\(\frac{m}{n}\)倍で運転すると、銅損は定格負荷の\((\frac{m}{n})^2\)倍になる。
- \(P_i=P_C\)の時、効率ηは最大になる。
$$\Large{P_{\frac{m}{n}}=(\frac{m}{n})^2P_C}$$
$$\Large{η_{\frac{m}{n}}=\frac{\frac{m}{n}V_{2n}I_{2n}cosθ}{\frac{m}{n}V_{2n}I_{2n}cosθ+P_i+(\frac{m}{n})^2P_C}×100}$$
\(V_{2n}\):定格時の二次電圧[V] \(I_{2n}\):定格時の二次電流[A] \(P_i\):鉄損[W] \(P_c\):銅損[W]
出力と電圧
出力
- 出力Pが上昇すると、銅損は上昇する。
$$\Large{P’_C=P_C×(\frac{P’}{P})^2}$$
\(P’_C\):変化後の銅損[W] \(P_C\):変化前の銅損[W] \(P’\):変化後の容量[W] \(P\):変化前の容量[W]
電圧
- 電圧Vが上昇すると、銅損は低下する。
$$\Large{P’_C=P_C×(\frac{V}{V’})^2}$$
\(P’_C\):変化後の銅損[W] \(P_C\):変化前の銅損[W] \(P’\):変化後の電圧[V] \(P\):変化前の電圧[V]
全日効率
$$\Large{η_d=\frac{PcosθT}{PcosθT+24P_i+P_CT}×100}$$
\(η_d\):全日効率[%] \(P\):定格時の容量[W] \(cosθ\):力率 \(T\):時間[h] \(P_i\):鉄損[W] \(P_c\):銅損[W]
変圧器の平行運転の条件
極性が一致している
- 極性(加極性、減極性)が一致していないと、大きな循環電流が流れる。
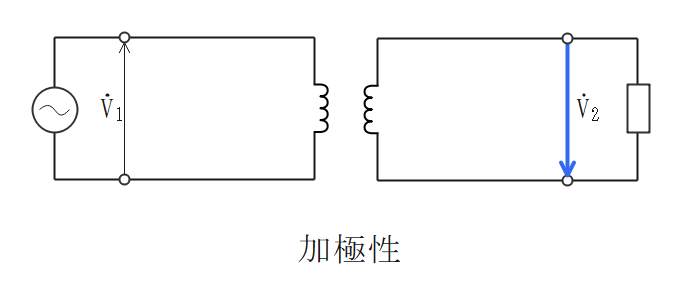
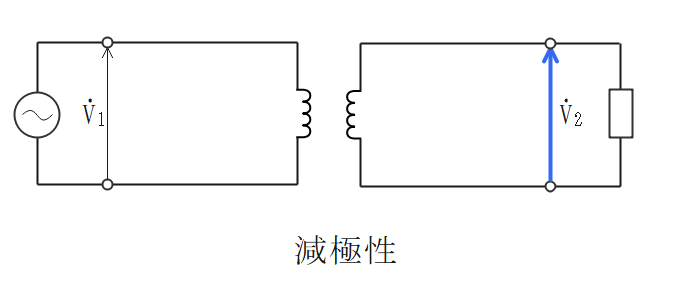
変圧比、巻数比、電流比が等しい
- 変圧比、巻数比、電流比が等しくないと、一次側と二次側に電圧差が生じるため循環電流が流れる。
百分率インピーダンス(%Z)が等しい
- 百分率インピーダンス(%Z)が等しくないと、電流を定格出力に比例するように分配できない。
$$\Large{%Z=\frac{I_nZ}{V_n}×100}$$
\(%Z\):百分率インピーダンス[%] \(I_n\):定格時の電流[A] \(V_n\):定格時の電圧[V]
rとxの比が等しい
- rとxの比(\(\frac{r}{x}\))が等しくないと、電流に位相差が生じて負荷供給電流が減少する。
短絡インピーダンス
- 負荷\(Z_L\)以外の抵抗(r,x)の合計
短絡電流
$$\Large{I_S=\frac{100}{%Z}×I_{1n}}$$
\(I_S\):短絡電流[A] \(%Z\):百分率インピーダンス[%] \(I_n\):定格電流[A]
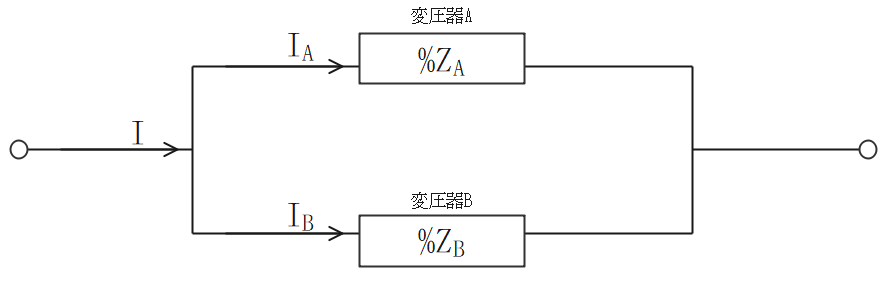
平行運転時の分担電流
- 変圧器Bを変圧器Aに換算した式を以下に示す。
$$\Large{I_A=I×\frac{%Z’_B}{%Z_A+%Z’_B}}$$
$$\Large{I_B=I×\frac{%Z_A}{%Z_A+%Z’_B}}$$
$$\Large{%Z’_B=%Z_B×\frac{P_(An)}{P_(Bn)}}$$
変圧器の三相結線と特徴
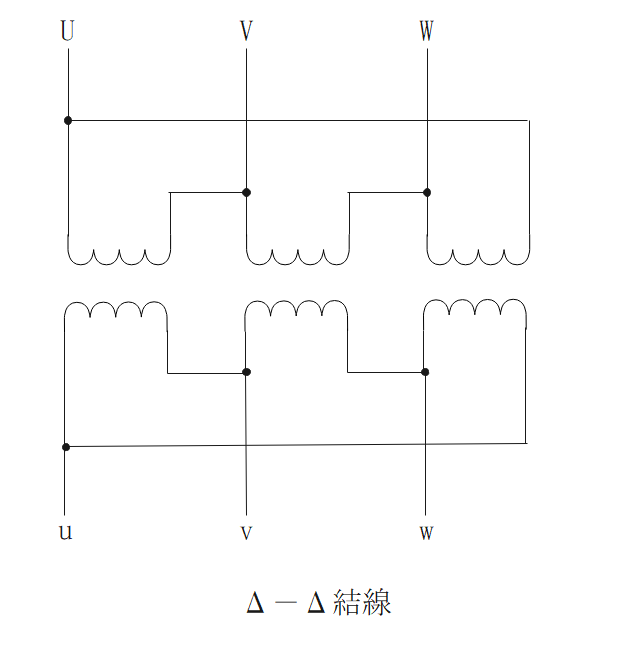
Δ-Δ結線
- 第3調波電流(ひずみ波)を出さない。
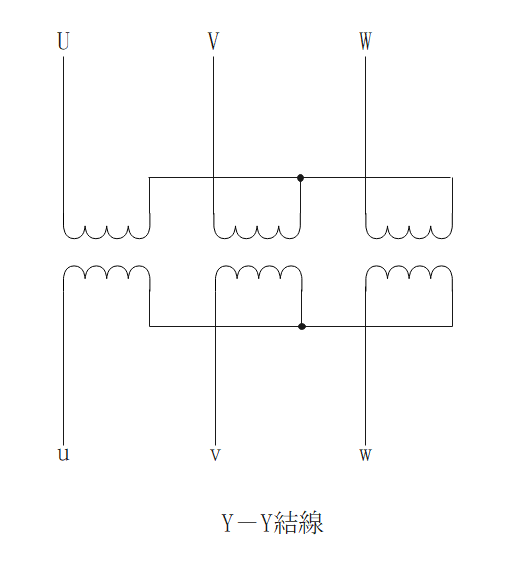
Y-Y結線
- 中性点接地ができる。
Δ-Y、Y-Δ結線
- 第3調波電流(ひずみ波)を出さず、中性点接地もできる。
ただし一次側と二次側の線間電圧に\(\frac{π}{6}\)radの位相差が生じる。
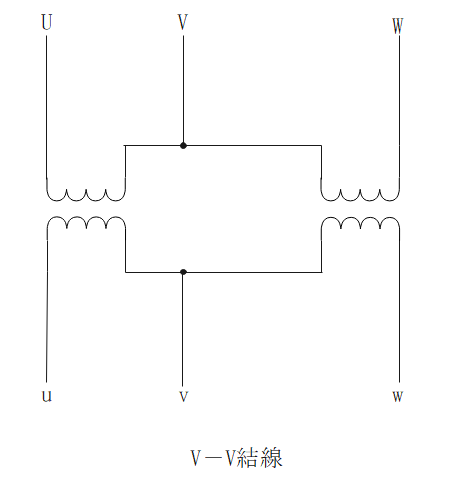
V-V結線
- 変圧器2台で結線が可能。ただし利用率が低い(0.866)
出力比
$$\Large{出力比=\frac{V-Vの出力}{Δ-Δの出力}=\frac{\sqrt{3}P}{3P}=\frac{\sqrt{3}}{3}}$$
各容量
自己容量
- 単巻変圧器自身の容量を示す。
$$\Large{P_S=V_1I_3=(V_2-V_1)I_2}$$
負荷容量
- 単巻変圧器の負荷に供給できる皮相電力を示す。
$$\Large{P_l=V_2I_2=V_1I_1}$$
各比の関係性
$$\Large{\frac{N_1}{N_2}=\frac{I_2}{I_3}=\frac{I_2}{I_1-I_2}}$$
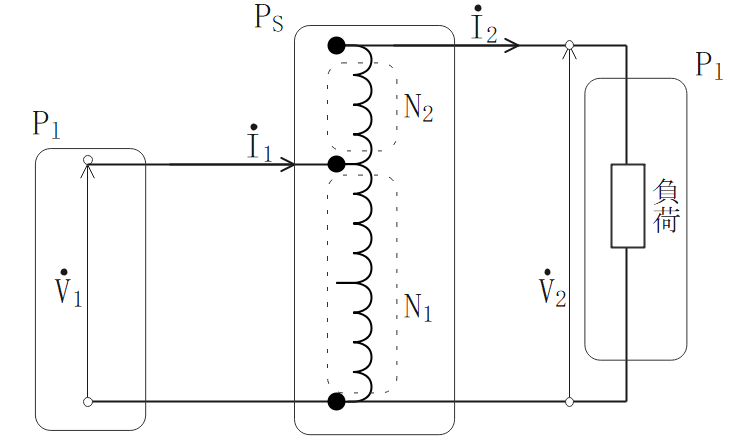
単巻変圧器の特徴
- 分路巻線が共通なため漏れ磁束が少ない。
- 電圧変動率が小さい。
- 小型かつ安価。
- 損失が少ない。


