電力その１０ 電力計算(Power Calculation)
このページでは、電力計算の公式や重要単語とその解説について掲載しています。
また、その公式がどの過去問に使われているかについても記載しています。
電力計算の分野では、パーセントインピーダンスや電線路の電力低下や電圧降下を求める計算問題が中心に出題されます。
電力科目の中でも計算の割合が多い分野です。そのため、過去問を多く解いて慣れる必要があります。
パーセントインピーダンス
パーセントインピーダンスは定格容量に比例する。
$$\Large{％Z = \frac{ZI_n}{E_n}×100=\frac{ZP_n}{(E_n)^2}×100}$$
定格容量
$$\Large{P_n = \sqrt{3}V_nI_ncosθ=一定}$$
パーセントインピーダンスの基準容量換算
$$\Large{％Z’ = \frac{P_B}{P_n}×％Z}$$
パーセント抵抗
$$\Large{％R = \frac{RI_n}{E_n}×100}$$
パーセントリアクタンス
$$\Large{％X = \frac{XI_n}{E_n}×100}$$
%Z、%R、%Xの関係
$$\Large{％Z^2 = ％R^2+％X^2}$$
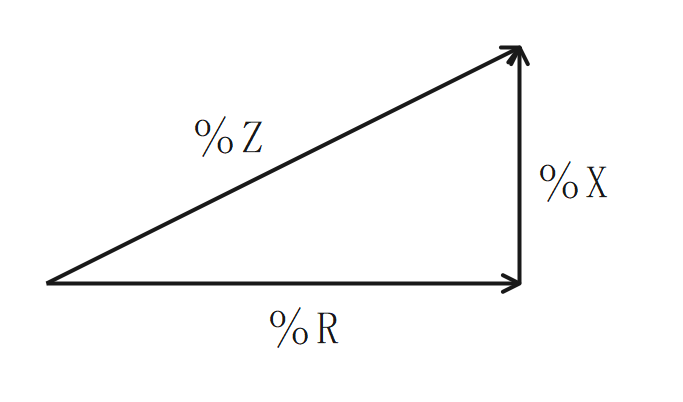
%Z、%R、%Xの合成計算
- %Z、%R、%Xの合成計算は、直列回路の抵抗の合成計算と同じ。
三相短絡電流
$$\Large{I_S = \frac{E_n}{Z_S}=\frac{100}{％Z_S}I_n=\frac{100}{％Z’_S}I’_n}$$
基準容量変換後の定格電流
$$\Large{I’_n=\frac{P_B}{P_n}×I_n}$$
受電端の三相電力
$$\Large{P= \frac{V_SV_r}{X}sinδ}$$
三相３線式(送電線路)の電力損失
$$\Large{P_l= 3RI^2=3R(\frac{P}{\sqrt{3}V_rcosθ})^2}$$
電圧降下率
配線中に発生する電圧降下の受電電圧に対する割合
$$\Large{ε= \frac{V_S-V_r}{V_r}×100}$$
三相３線式の電圧降下
$$\Large{v=V_S-V_r=\sqrt{3}I(Rcosθ+Xsinθ)=\frac{PR+QX}{V_r}}$$
三相２線式の電圧降下
$$\Large{v=V_S-V_r=2I(Rcosθ+Xsinθ)}$$
無負荷充電電流
$$\Large{I_C=\frac{\frac{V}{\sqrt{3}}}{X_C}}$$
三相分の無負荷充電容量
$$\Large{Q_C=\sqrt{3}VI_C}$$
三相分の誘電損
交流電界を誘電体に加えたときに、その交流電界より位相が遅れて分極が発生し、熱エネルギーがによる損失が生じる。。
$$\Large{P_d=2πfCV_l^2tanδ}$$
この記事が気に入ったら
いいねしてね！